Question

已知圆C的圆心在直线l：3x-y=0上，且与直线l₁：x-y+4=0相切．
（1）若直线x-y=0截圆C所得弦长为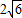，求圆C的方程．
（2）若圆C与圆x²+y²-4x-12y+8=0外切，试求圆C的半径．
（3）满足已知条件的圆显然不只一个，但它们都与直线l₁相切，我们称l₁是这些圆的公切线．这些圆是否还有其他公切线？若有，求出公切线的方程，若没有，说明理由．

Answer 1

【答案】分析：（1）设圆C的圆心坐标为（a，3a），则它的半径，C到直线x-y=0的距离，由此能求出圆C的方程．
（2）两圆的连心线长为，由两圆外切，能求出圆C的半径．
（3）如果存在另一条公切线，则它必过l与l₁的交点（2，6），分斜率不存在和斜率存在两种情况进行讨论，能求出还存在一条切线，其方程为7x+y-20=0．
解答：解：（1）设圆C的圆心坐标为（a，3a），
则它的半径
C到直线x-y=0的距离，
因而圆C截该直线所得弦长为，
∴
圆C的方程为
（2）两圆的连心线长为，
因为两圆外切，所以，
∴
（3）如果存在另一条公切线，则它必过l与l₁的交点（2，6），
①若斜率不存在，则其方程为x=2，
圆心C到它的距离|a-2|=r=|a-2|，
由于方程需要对任意的a都成立，因此无解，
所以它不是公切线．
②若斜率存在，设公切线为y-6=k（x-2），即kx-y+6-2k=0，
∴d==r=，
∴k²+6k-7=0，
解出k=1或k=-7．
k=1时与直线l₁重合，k=-7时，直线方程为7x+y-20=0．
∴还存在一条切线，其方程为7x+y-20=0．
点评：本题考查圆的方程的求法，考查圆的半径的求法，考查圆的切线方程的求法，解题时要认真审题，仔细解答，注意合理地进行等价转化．