题目内容
已知圆C的半径为2,圆心在x轴正半轴上,直线3x-4y+4=0与圆C相切
(1)求圆C的方程
(2)过点Q(0,-3)的直线l与圆C交于不同的两点A(x1,y1),B(x2,y2)且为x1x2+y1y2=3时求:△AOB的面积.
(1)求圆C的方程
(2)过点Q(0,-3)的直线l与圆C交于不同的两点A(x1,y1),B(x2,y2)且为x1x2+y1y2=3时求:△AOB的面积.
分析:(I)设圆心为C(a,0),(a>0),可得圆C的方程的方程.再根据圆心到直线的距离等于半径求得a的值,可得圆C的方程.
(II)依题意:设直线l的方程为:y=kx-3,代入圆的方程化简,里哦也难怪根与系数的关系求得x1+x2=
,x1x2=
,再由x1x2+y1y2=3,求得k的值,可得∴直线l的方程.求得圆心C到l的距离d、以及|AB|的值,再由S△AOB=
|AB|•h,计算求得结果.
(II)依题意:设直线l的方程为:y=kx-3,代入圆的方程化简,里哦也难怪根与系数的关系求得x1+x2=
| 4+6k |
| 1+k2 |
| 9 |
| 1+k2 |
| 1 |
| 2 |
解答:解:(I)设圆心为C(a,0),(a>0),则圆C的方程为(x-a)2+y2=4.
因为圆C与3x-4y+4=0相切,所以
=2,解得:a=2或a=-
(舍),
所以圆C的方程为:(x-2)2+y2=4.…(4分)
(II)依题意:设直线l的方程为:y=kx-3,由
得(1+k2)x2-(4+6k)x+9=0,
∵l与圆C相交于不同两点A(x1,y1),B(x2,y2),
∴△=(4+6k2)-4(1+k2)×9>0,且x1+x2=
,x1x2=
,
∴y1y2=(kx1-3)(kx2-3)=k2•x1x2-3k(x1x2)+9=
-
+9,
又∵x1x2+y1y2=3,∴
+
-
+9=3,
整理得:k2+4k-5=0解得k=1或k=-5(舍).
∴直线l的方程为:y=x-3.…(8分)
圆心C到l的距离d=
=
,在△ABC中,∵|AB|=2•
=14,
原点O到直线l的距离,即△AOB底边AB边上的高h=
=
,
∴S△AOB=
|AB|•h=
•
•
=
.…(12分)
因为圆C与3x-4y+4=0相切,所以
| |3a+4| | ||
|
| 14 |
| 3 |
所以圆C的方程为:(x-2)2+y2=4.…(4分)
(II)依题意:设直线l的方程为:y=kx-3,由
|
∵l与圆C相交于不同两点A(x1,y1),B(x2,y2),
∴△=(4+6k2)-4(1+k2)×9>0,且x1+x2=
| 4+6k |
| 1+k2 |
| 9 |
| 1+k2 |
∴y1y2=(kx1-3)(kx2-3)=k2•x1x2-3k(x1x2)+9=
| 9k2 |
| 1+k2 |
| 12k+18k2 |
| 1+k2 |
又∵x1x2+y1y2=3,∴
| 9k2 |
| 1+k2 |
| 9k2 |
| 1+k2 |
| 12k+18k2 |
| 1+k2 |
整理得:k2+4k-5=0解得k=1或k=-5(舍).
∴直线l的方程为:y=x-3.…(8分)
圆心C到l的距离d=
| |2-3| | ||
|
| ||
| 2 |
22-
|
原点O到直线l的距离,即△AOB底边AB边上的高h=
| 3 | ||
|
| 3 |
| 2 |
| 2 |
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 14 |
3
| ||
| 2 |
| 3 |
| 2 |
| 7 |
点评:本题主要考查直线和圆相交的性质,求圆的标准方程,一元二次方程根与系数的关系,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知圆C的半径为2,圆心在x轴的正半轴上,直线3x+4y+4=0与圆C相切,则圆C的方程为( )
| A、x2+y2-2x-3=0 | B、x2+y2+4x=0 | C、x2+y2+2x-3=0 | D、x2+y2-4x=0 |
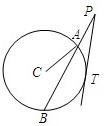 (选做题)(几何证明选讲)如图所示,过圆C外一点P做一条直线与圆C交于A,B两点,BA=2AP,PT与圆C相切于T点.已知圆C的半径为2,∠CAB=30°,则PT=
(选做题)(几何证明选讲)如图所示,过圆C外一点P做一条直线与圆C交于A,B两点,BA=2AP,PT与圆C相切于T点.已知圆C的半径为2,∠CAB=30°,则PT= 与圆C相切.
与圆C相切. 与圆C交于不同的两点A
与圆C交于不同的两点A 、B
、B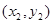 ,当
,当 时,求△AOB的面积.
时,求△AOB的面积.