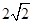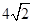题目内容
已知双曲线方程为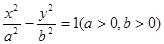
，椭圆C以该双曲线的焦点为顶点，顶点为焦点。
（1）当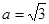
，
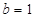时，求椭圆C的方程；
（2）在（1）的条件下，直线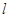
：
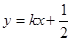与
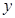轴交于点P，与椭圆交与A，B两点，若O为坐标原点，
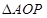与
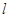面积之比为2：1，求直线的方程；
（3）若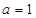
，椭圆C与直线
：
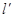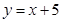有公共点，求该椭圆的长轴长的最小值。
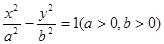，椭圆C以该双曲线的焦点为顶点，顶点为焦点。（1）当
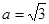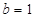，时，求椭圆C的方程；（2）在（1）的条件下，直线
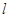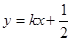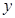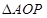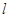：与轴交于点P，与椭圆交与A，B两点，若O为坐标原点，与面积之比为2：1，求直线的方程；（3）若
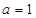，椭圆C与直线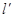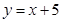：有公共点，求该椭圆的长轴长的最小值。解：（1）设双曲线的焦点为
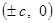
，则椭圆C的方程为
，其中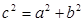
将
代入，可得椭圆C的方程为
；（2）根据题意，设点A，B的坐标分别为
，则
，可知。
联立椭圆和直线的方程，得
，消元得
，可知
，
，即
异号，所以
。代入上式，得
消元，得
。所以直线方程为
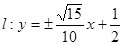
（3）联立椭圆和直线的方程，得方程组
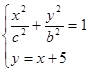，其中
，消去
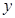，得到方程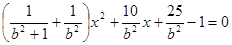
，因为椭圆与直线有公共点，所以
△
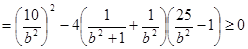，解得
，所以
，当且仅当
时长轴长最短，是
。略
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
的两条渐近线与直线
围成的三角形区域（包括边界）为D，P
为D内的一个动点，则目标函数
的最小值为（ ）
，
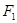是双曲线的两个焦点，过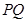
交双曲线于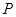
，
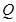两点，若∠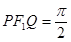
，则双曲线的离心率
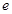等于（ ）
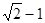
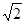
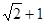
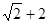
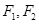是双曲线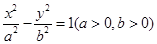
的焦点，若在双曲线上存在点P，使得
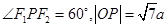，则双曲线的渐近线方程为（ ）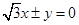
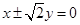
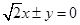
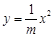的焦点坐标为 ▲ .
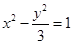的渐近线方程为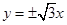
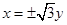
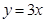
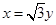
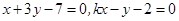与两坐标轴围成的四边形内接于一个圆，则实数
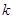为（ ）
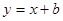与曲线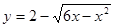
有公共点，则
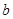的取值范围是（ ）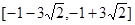
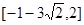
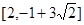
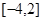
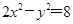的实轴长是（ ）
