题目内容
【题目】设函数![]() ,已知
,已知![]() 在
在![]() 处的切线
处的切线![]() 相同.
相同.
(1)求![]() 的值及切线
的值及切线![]() 的方程;
的方程;
(2)设函数![]() ,若存在实数
,若存在实数![]() 使得关于
使得关于![]() 的不等式
的不等式![]() 对
对![]() 上的任意实数
上的任意实数![]() 恒成立,求
恒成立,求![]() 的最小值及对应的
的最小值及对应的![]() 的解析式.
的解析式.
【答案】(1)![]() ,
,![]() (2)
(2)![]() 的最小值为2,
的最小值为2,![]()
【解析】
试题分析:(1)由导数几何意义得![]() ,又切点相同,所以
,又切点相同,所以![]() ,从而可列方程组
,从而可列方程组![]() 且
且![]() ,解得
,解得![]() ,
,![]() ,再根据点斜式得切线方程:
,再根据点斜式得切线方程:![]() (2)由题意可得
(2)由题意可得![]() 为函数
为函数![]() 的一条公切线,先求公切线,易得:
的一条公切线,先求公切线,易得:![]() ,解得
,解得![]() 公切线为
公切线为![]() ,再证
,再证![]() 恒成立
恒成立
试题解析:解:(1)![]() ,
,
由已知![]() 且
且![]() ,
,
∴![]() 且
且![]() ,得
,得![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴切线![]() 的方程为
的方程为![]() , 即
, 即![]()
(2)由(1)知,![]() ,又因为
,又因为![]() ,
,
可知![]() ,
,
①由![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,
恒成立,
所以![]() ,解得
,解得![]() ①
①
②由![]() 对
对![]() 恒成立,即设
恒成立,即设![]() ,
,
则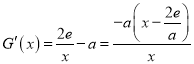 ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 单调递减,
单调递减,
故![]() ,
,
则![]() ,故得
,故得![]() ,②
,②
由①②得![]() ,③
,③
由存在实数![]() 使得③成立的充要条件 是:不等式
使得③成立的充要条件 是:不等式![]() ,有解,该不等式可化为
,有解,该不等式可化为![]() 有解
有解
令![]() ,则有
,则有![]() ,设
,设![]() ,
,
 ,
,
可知![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
又![]() ,所以
,所以![]() 在区间
在区间![]() 内存在一个零点
内存在一个零点![]() ,故不等式
,故不等式![]() 的解为
的解为![]() 即
即![]() ,得
,得![]() ,
,
因此![]() 的最小值为2,代入③中得
的最小值为2,代入③中得![]() ,故
,故![]() ,此时对应的
,此时对应的![]() 的解析式为
的解析式为![]()

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目