题目内容
已知集合M={y|y=x2+2x-3，x∈R}，集合N={x|-1≤x≤5}，则M∩N=（ ）
| A、{y|y≥-4} |
| B、{y|-1≤y≤5} |
| C、{y|-4≤y≤-1} |
| D、φ |
考点：交集及其运算
专题：集合
分析：根据二次函数的图象和性质，求出集合M，结合集合交集的定义，可得答案．
解答：
解：∵M={y|y=x2+2x-3，x∈R}={y|x≥-4}，
集合N={y|-1≤y≤5}，
∴M∩N={y|-1≤y≤5}，
故选：B
集合N={y|-1≤y≤5}，
∴M∩N={y|-1≤y≤5}，
故选：B
点评：本题考查的知识点是集合的交集，交集，补集运算，难度不大，属于基础题
练习册系列答案
名校课堂系列答案
相关题目
△ABC的三个内角为A，B，C，若
=tan
，则sin（B+C）=（ ）
sinA+
| ||
cosA-
|
| 5π |
| 6 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
cos（-420°）等于（ ）
| A、0 | ||||
B、
| ||||
C、
| ||||
| D、1 |
函数y=log4（1+x2+2x）的图象大致是（ ）
A、 |
B、 |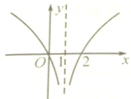
C、 |
D、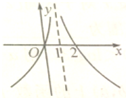 |