题目内容
在△ABC中,角A,B,C的对边分别为a,b,c.已知3cos(B-C)-1=6cosBcosC.
(1)求cosA; (2)若a=3,△ABC的面积为2 ,求b,c.
,求b,c.
解:(1)∵3(cosBcosC+sinBsinC)-1=6cosBcosC,
∴3cosBcosC-3sinBsinC=-1,∴3cos(B+C)=-1,
∴cos(π-A)=- ,∴cosA=
,∴cosA= .
.
(2)由(1)得sinA= ,由面积公式
,由面积公式 bcsinA=2
bcsinA=2 可得bc=6,①
可得bc=6,①
根据余弦定理得cosA= =
= =
= ,则b2+c2=13, ②
,则b2+c2=13, ②
①、②两式联立可得b=2,c=3或b=3,c=2.

练习册系列答案
相关题目
 +x-2在P0点处的切线平行于直线y=4x-1,则P0点坐标为( )
+x-2在P0点处的切线平行于直线y=4x-1,则P0点坐标为( ) ,
, ,函数
,函数 若
若 ,且
,且 , 则
, 则 的取值范围是
的取值范围是 ] (B) (
] (B) ( ] (C)(
] (C)( ]
] 构成一个等比数列,则圆锥曲线
构成一个等比数列,则圆锥曲线 的离心率为( )
的离心率为( ) 或
或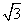 (B)
(B)
 ⊥平面
⊥平面 ,四边形
,四边形 ,
, 是
是 的中点,则
的中点,则 与平面
与平面 所成角的正弦值为 ( ).
所成角的正弦值为 ( ). B.
B.  C.
C.  D.
D. 
 的焦点为F,经过点F的直线与抛物线交于
的焦点为F,经过点F的直线与抛物线交于 两点.
两点. ,求线段
,求线段 中点
中点 的轨迹方程;
的轨迹方程; 的方向向量为
的方向向量为 ,当焦点为
,当焦点为 时,求
时,求 的面积;
的面积; 准线上的点,求证:直线
准线上的点,求证:直线 的斜率成等差数列.
的斜率成等差数列. 的正三角形,则原三角形的面积是
的正三角形,则原三角形的面积是




 的图象上所有的点向左平移
的图象上所有的点向左平移 个单位长度,再把图象上各点的横坐标扩大到原来的2倍,则所得的图象的解析式为( )
个单位长度,再把图象上各点的横坐标扩大到原来的2倍,则所得的图象的解析式为( )  B.
B.
 D.
D.