题目内容
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,圆
轴的正半轴重合,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为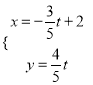 (
(![]() 为参数).
为参数).
(Ⅰ)若![]() ,
, ![]() 是直线
是直线![]() 与
与![]() 轴的交点,
轴的交点, ![]() 是圆
是圆![]() 上一动点,求
上一动点,求![]() 的最大值;
的最大值;
(Ⅱ)若直线![]() 被圆
被圆![]() 截得的弦长等于圆
截得的弦长等于圆![]() 的半径
的半径![]() 倍,求
倍,求![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)首先,根据所给a的值,将圆的极坐标方程化为普通方程,将直线的参数方程化为直角坐标方程,然后,根据圆的性质,将所求的最值转化为到圆心的距离;(Ⅱ)首先,得到原点普通方程,然后,结合圆的弦长公式,建立关系式求解a的值即可.
试题解析:
(Ⅰ)当![]() 时,圆
时,圆![]() 的极坐标方程为
的极坐标方程为![]() ,可化为
,可化为![]() ,
,
化为直角坐标方程为![]() ,即
,即![]() .
.
直线![]() 的普通方程为
的普通方程为![]() ,与
,与![]() 轴的交点
轴的交点![]() 的坐标为
的坐标为![]() ,
,
∵圆心![]() 与点
与点![]() 的距离为
的距离为![]() ,
,
∴![]() 的最大值为
的最大值为![]() .
.
(Ⅱ)由![]() ,可化为
,可化为![]() ,
,
∴圆![]() 的普通方程为
的普通方程为![]() .
.
∵直线![]() 被圆
被圆![]() 截得的弦长等于圆
截得的弦长等于圆![]() 的半径的
的半径的![]() 倍,
倍,
∴由垂径定理及勾股定理得:圆心到直线![]() 的距离为圆
的距离为圆![]() 半径的一半,
半径的一半,
∴ ,解得
,解得![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知某产品的历史收益率的频率分布直方图如图所示:
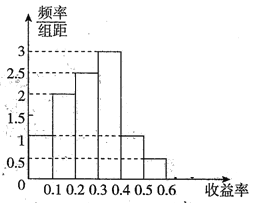
(1)试计算该产品收益率的中位数;
(2)若该产品的售价![]() (元)与销量
(元)与销量![]() (万件)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组
(万件)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组![]() 与
与![]() 的对应数据:
的对应数据:
售价 | 25 | 30 | 38 | 45 | 52 |
销量 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
据此计算出的回归方程为![]() ,求
,求![]() 的值;
的值;
(3)若从上述五组销量中随机抽取两组,求两组销量中恰有一组超过6万件的概率.