题目内容
已知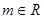 ,对
,对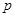 :
: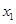 和
和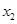 是方程
是方程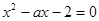 的两个根,不等式
的两个根,不等式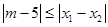 对任意实数
对任意实数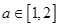 恒成立;
恒成立;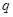 :函数
:函数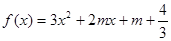 有两个零点,求使“
有两个零点,求使“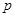 且
且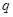 ”为真命题的实数的取值范围。
”为真命题的实数的取值范围。
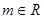 ,对
,对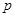 :
: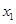 和
和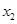 是方程
是方程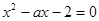 的两个根,不等式
的两个根,不等式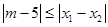 对任意实数
对任意实数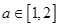 恒成立;
恒成立;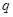 :函数
:函数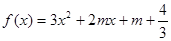 有两个零点,求使“
有两个零点,求使“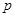 且
且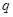 ”为真命题的实数的取值范围。
”为真命题的实数的取值范围。
试题分析:利用二次方程的韦达定理求出|x1-x2|,将不等式恒成立转化为求函数的最值,求出命题p为真命题时m的范围;利用二次方程有两个不等根判别式大于0,求出命题Q为真命题时m的范围;P且Q为真转化为两个命题全真,求出m的范围.解:由题设x1+x2=a,x1x2=-2,∴|x1-x2|=
 .当a∈[1,2]时,
.当a∈[1,2]时, 的最小值为3.要使|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立,只须|m-5|≤3,即2≤m≤8.由已知,得f(x)=3x2+2mx+m+
的最小值为3.要使|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立,只须|m-5|≤3,即2≤m≤8.由已知,得f(x)=3x2+2mx+m+ =0的判别式△=4m2-12(m+
=0的判别式△=4m2-12(m+ )=4m2-12m-16>0,得m<-1或m>4.综上,要使“p且q”为真命题,只需P真Q真,即2≤m≤8,m<-1或m>4,解得实数m的取值范围是(4,8].
)=4m2-12m-16>0,得m<-1或m>4.综上,要使“p且q”为真命题,只需P真Q真,即2≤m≤8,m<-1或m>4,解得实数m的取值范围是(4,8].点评:本题考查二次方程的韦达定理、二次方程有根的判断、复合命题的真假与构成其简单命题的真假的关系.

练习册系列答案
相关题目
 :对任意
:对任意 ,
, 的否定是( )
的否定是( ) :对任意
:对任意
 ,
,

 ,命题
,命题 ,若命题“
,若命题“ ”为真命题,则实数
”为真命题,则实数 的取值范围是 ( )
的取值范围是 ( ) 



 ,则
,则 成等比数列
成等比数列 ,使得
,使得 成立
成立 ,满足
,满足 ,则
,则 或
或
 ,则
,则
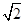 的正方形,AE⊥平面ABCD,BF∥AE且AE=2BF=4,则以下结论正确的是______________________.(写出所有正确结论的编号)
的正方形,AE⊥平面ABCD,BF∥AE且AE=2BF=4,则以下结论正确的是______________________.(写出所有正确结论的编号)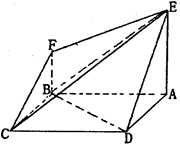
 =2—3x,变量x增加一个单位时,y平均增加3个单位;
=2—3x,变量x增加一个单位时,y平均增加3个单位; ”的否定
”的否定 P:“
P:“ ”;
”; -p;
-p;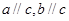 ,那么
,那么 可以确定一个平面;(2)如果直线
可以确定一个平面;(2)如果直线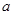 和
和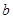 都与直线
都与直线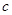 相交,那么
相交,那么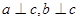 那么
那么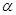 内一点与平面外一点,直线
内一点与平面外一点,直线 ,使得
,使得
 的值为2;
的值为2; ,则
,则 与
与 的夹角为钝角;
的夹角为钝角; ,则不等式
,则不等式 成立的概率是
成立的概率是 ;
; 的最小值为2.
的最小值为2.