题目内容
已知正项数列 在抛物线
在抛物线 上;数列
上;数列 中,点
中,点 在过点(0,1),以
在过点(0,1),以 为斜率的直线上。
为斜率的直线上。
(1)求数列 的通项公式;
的通项公式;
(2)若 成立,若存在,求出k值;若不存在,请说明理由;
成立,若存在,求出k值;若不存在,请说明理由;
(3)对任意正整数 ,不等式
,不等式 恒成立,求正数
恒成立,求正数 的取值范围。
的取值范围。
【答案】
(1)

(2)k=4
(3)
【解析】
试题分析:解:(1)将点 代入
代入 中得
中得

直线l: 

(2) 
当k为偶数时,k+27为奇数

k=4
当k为奇数时,k+27为偶数
 舍去
舍去
(Ⅲ)由
即 9分
9分
记


 递增 13分
递增 13分

 14分
14分
考点:函数与数列
点评:主要是考查了函数为背景的数列 的通项公式以及数列的单调性的运用,属于难度题。

练习册系列答案
相关题目
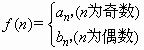 ,问是否存在k∈N,使f(k+27)=4f(k)成立,若存在,求出k值;若不存在,请说明理由;
,问是否存在k∈N,使f(k+27)=4f(k)成立,若存在,求出k值;若不存在,请说明理由;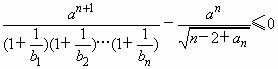 恒成立,求正数a的取值范围.
恒成立,求正数a的取值范围.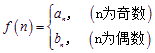 ,问是否存在
,问是否存在 成立,求正数
成立,求正数 ,问是否存在
,问是否存在 成立,求正数
成立,求正数