题目内容
已知点M(3,1),直线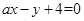 与圆
与圆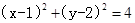 。
。
(1)求过点M的圆的切线方程;
(2)若直线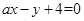 与圆相切,求a的值;
与圆相切,求a的值;
(3)若直线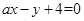 与圆相交与A,B两点,且弦AB的长为
与圆相交与A,B两点,且弦AB的长为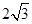 ,求a的值。
,求a的值。
【答案】
(1)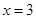 和
和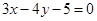 (2)
(2)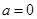 或
或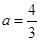 (3)
(3)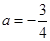
【解析】
试题分析:(1)点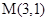 在圆
在圆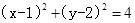 外,故切线有两条件,当斜率不存在时即
外,故切线有两条件,当斜率不存在时即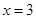 时满足与M相切,当斜率存在时可设点斜式直线方程
时满足与M相切,当斜率存在时可设点斜式直线方程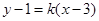 ,再由圆心到直线的距离等于半径求出
,再由圆心到直线的距离等于半径求出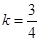 由此能求出两条件切线方程.
由此能求出两条件切线方程.
(2)由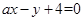 与圆相切知圆心到直线的距离等于半径得
与圆相切知圆心到直线的距离等于半径得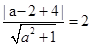 ,由此能求出a.
,由此能求出a.
(3)圆心到直线的距离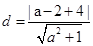 ,圆的半径
,圆的半径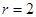 ,由
,由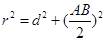 ,能求出a.
,能求出a.
试题解析:
(1)圆心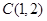 ,半径
,半径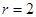 ,当切线的斜率不存在是,方程为
,当切线的斜率不存在是,方程为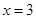 .由圆心
.由圆心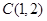 到直线
到直线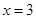 的距离
的距离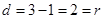 知,此时直线与圆相切。
知,此时直线与圆相切。
当切线的斜率存在时,设切线方程为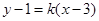 ,
,
即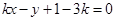 .
.
由题意知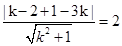 ,解得k=
,解得k=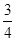 ,
,
∴切线方程为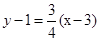 ,即
,即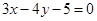 .
.
故国M点的圆的切线方程为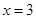 和
和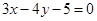 .
.
(2)由题意知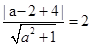 ,解得
,解得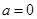 或
或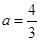
(3)∵圆心到直线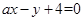 的距离为
的距离为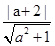
∴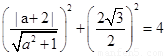
 解得
解得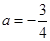 .
.
考点:直线和圆的方程的应用;圆的切线方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目