题目内容
已知点M(3,1),圆(x-1)2+(y-2)2=4.
(1)求过M点的圆的切线方程;
(2)若直线ax-y+4=0与圆相交于A、B两点,且弦AB的长为2
,求a的值.
(1)求过M点的圆的切线方程;
(2)若直线ax-y+4=0与圆相交于A、B两点,且弦AB的长为2
| 3 |
分析:(1)由圆的方程找出圆心坐标与半径,分两种情况考虑:若切线方程斜率不存在,直线x=3满足题意;若斜率存在,设出切线方程,根据直线与圆相切时圆心到切线的距离d=r,求出k的值,综上即可确定出满足题意的切线方程;
(2)由AB弦长,以及圆的半径,利用点到直线的距离公式,根据垂径定理及勾股定理列出关于a的方程,求出方程的解即可得到a的值.
(2)由AB弦长,以及圆的半径,利用点到直线的距离公式,根据垂径定理及勾股定理列出关于a的方程,求出方程的解即可得到a的值.
解答:解:(1)由圆的方程得到圆心(1,2),半径r=2,
当直线斜率不存在时,方程x=3与圆相切;
当直线斜率存在时,设方程为y-1=k(x-3),即kx-y+1-3k=0,
由题意得:
=2,
解得:k=
,
∴方程为y-1=
(x-3),即3x-4y-5=0,
则过点M的切线方程为x=3或3x-4y-5=0;
(2)∵圆心到直线ax-y+4=0的距离d=
,
∴(
)2+(
)2=4,
解得:a=-
.
当直线斜率不存在时,方程x=3与圆相切;
当直线斜率存在时,设方程为y-1=k(x-3),即kx-y+1-3k=0,
由题意得:
| |k-2+1-3k| | ||
|
解得:k=
| 3 |
| 4 |
∴方程为y-1=
| 3 |
| 4 |
则过点M的切线方程为x=3或3x-4y-5=0;
(2)∵圆心到直线ax-y+4=0的距离d=
| |a+2| | ||
|
∴(
| |a+2| | ||
|
2
| ||
| 2 |
解得:a=-
| 3 |
| 4 |
点评:此题考查了直线与圆相交的性质,涉及的知识有:点到直线的距离公式,垂径定理,勾股定理,以及圆的标准方程,利用了分类讨论的思想,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,求a的值.
,求a的值.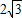 ,求a的值.
,求a的值.