题目内容
2．${cos^2}15°-\frac{1}{2}$=$\frac{\sqrt{3}}{4}$．分析 利用二倍角公式变形可得要求式子的值．
解答 解：∵${cos^2}15°-\frac{1}{2}=\frac{1}{2}（2{cos^2}15°-1）=\frac{1}{2}cos30°=\frac{{\sqrt{3}}}{4}$，
故答案为：$\frac{\sqrt{3}}{4}$．
点评 本题主要考查同角基本关系式和二倍角公式的应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
15．已知△ABC的两个顶点A（5，0），B（-5，0），周长为22，则顶点C的轨迹方程是（ ）
| A． | $\frac{x^2}{36}+\frac{y^2}{11}=1$ | B． | $\frac{x^2}{36}+\frac{y^2}{11}=1（{y≠0}）$ | ||
| C． | $\frac{x^2}{9}+\frac{y^2}{16}=1$ | D． | $\frac{x^2}{9}+\frac{y^2}{16}=1（{y≠0}）$ |
10．已知定义域为R的函数f（x）的图象经过点（1，1），且对?x∈R，都有f'（x）＞-2，则不等式$f（{log_2}|{3^x}-1|）＜3-{log_{\sqrt{2}}}|{3^x}-1|$的解集为（ ）
| A． | （-∞，0）∪（0，1） | B． | （0，+∞） | C． | （-1，0）∪（0，3） | D． | （-∞，1） |
7．集合A={-1，0，1，2，3}，B={x|log2（x+1）＜2}，则A∩B等于（ ）
| A． | {-1，0，1，2} | B． | {0，1，2} | C． | {-1，0，1，2，3} | D． | {0，1，2，3} |
13．
一个几何体的三视图如图所示，该几何体外接球的表面积为（ ）
一个几何体的三视图如图所示，该几何体外接球的表面积为（ ）| A． | 36π | B． | $\frac{112}{3}π$ | C． | 32π | D． | 28π |
满足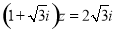
（
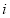为虚数单位），则
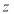在复平面内对应的点位于（ ）