题目内容
已知椭圆ax2+y2=4与
+
=1的焦距相等,则a=
或4
或4.
| x2 |
| 12 |
| y2 |
| 9 |
| 4 |
| 7 |
| 4 |
| 7 |
分析:先将椭圆C1:
+
=1标准方程,得到它的焦距2c,再将椭圆C2:ax2+y2=4化成标准方程,结合两个椭圆的焦距相等,所以椭圆C2的半焦距也是c,最后分焦点在x轴和y轴两种情况加以讨论,列出将于a的方程,再解之即可求出参数a的值.
| x2 |
| 12 |
| y2 |
| 9 |
解答:解:将椭圆C1:
+
=1标准方程
所以椭圆C1的半焦距为c=
=
,焦距为2c=2
再将椭圆C2:ax2+y2=4化成标准方程:
+
=1,
两个椭圆的焦距相等,所以椭圆C2的半焦距也是
,
接下来分两种情况讨论:
(1)当焦点在x轴上时,c=
=
,解之得a=
;
(2)当焦点在y轴上时,c=
=
,解之得a=4
综上所述,得a的值为
或4.
故答案为:
或4.
| x2 |
| 12 |
| y2 |
| 9 |
所以椭圆C1的半焦距为c=
| 12-9 |
| 3 |
| 3 |
再将椭圆C2:ax2+y2=4化成标准方程:
| x2 | ||
|
| y2 |
| 4 |
两个椭圆的焦距相等,所以椭圆C2的半焦距也是
| 3 |
接下来分两种情况讨论:
(1)当焦点在x轴上时,c=
|
| 3 |
| 4 |
| 7 |
(2)当焦点在y轴上时,c=
4-
|
| 3 |
综上所述,得a的值为
| 4 |
| 7 |
故答案为:
| 4 |
| 7 |
点评:本题在两个椭圆的焦距相等的情况下,求参数a的值,着重考查了椭圆的标准方程和椭圆的简单几何性质,属于基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
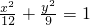 的焦距相等,则a=________.
的焦距相等,则a=________. 的焦距相等,则a= .
的焦距相等,则a= .