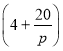题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,判断
,判断![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若![]() ,求
,求![]() 在
在![]() 上的最小值;
上的最小值;
(3)若![]() ,且
,且![]() 有三个不同实根,求
有三个不同实根,求![]() 的取值范围.
的取值范围.
【答案】(1)是奇函数;(2)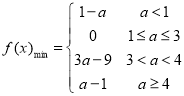 ;(3)
;(3)![]() .
.
【解析】
(1)由a=0,可得f(x)为奇函数,运用定义即可得到结论;
(2)求得f(x)的解析式,讨论a<1时,当1≤a≤3时,当3<a≤4时,当a>4时,结合单调性,可得最小值;
(3)由题意可得f(x)不单调,求得f(x)的分段函数,讨论当x≥a递增,且a≥0,x<a不单调,以及当x<a递增,且a<0,x≥a不单调,可得![]() 的范围,即可得到所求取值范围.
的范围,即可得到所求取值范围.
解:(1)a=0,可得f(x)=x|x|+bx为奇函数,
由定义域为R,f(﹣x)=﹣x|﹣x|﹣bx=﹣(x|x|+bx)=﹣f(x),
则f(x)为奇函数;
(2)b=0,可得f(x)=x|x﹣a|
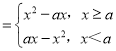 ,
,
由于1≤x≤3,
当a<1时,可得f(x)=x2﹣ax在[1,3]递增,
可得f(x)的最小值为f(1)=1﹣a;
当a>3时,f(x)=ax﹣x2在[1,![]() ]递增,(
]递增,(![]() ,3]递减,
,3]递减,
由f(1)﹣f(3)═a﹣1﹣(3a﹣9)=8﹣2a,
可得a>4时,f(1)<f(3),即为f(1)取得最小值a﹣1;
当3<a≤4时,f(1)≥f(3),可得f(3)取得最小值3a﹣9;
当1≤a≤3时,由f(x)≥0,可得x=a时,取得最小值0,
综上可得,a<1时,f(x)的最小值为1﹣a;
当1≤a≤3时,f(x)的最小值为0;
当3<a≤4时,f(x)的最小值为3a﹣9;
当a>4时,f(x)的最小值为a﹣1;
(3)b>0,且f(x)![]() 有三个不同实根,
有三个不同实根,
则f(x)不单调,
且f(x)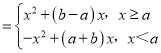 ,
,
当x≥a递增,且a≥0,x<a不单调,
可得![]() a,成立,又
a,成立,又![]() a,即a>b;
a,即a>b;
即ab![]() ,
,
即3ab<a2+b2<6ab,
则![]() 的取值范围是(
的取值范围是(![]() ,
,![]() );
);
当x<a递增,且a<0,x≥a不单调,
可得![]() a即a<﹣b,又
a即a<﹣b,又![]() a,即a≤b;
a,即a≤b;
即有![]() ab,不成立.
ab,不成立.
综上可得![]() 的取值范围是(
的取值范围是(![]() ,
,![]() ).
).

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】汽车智能辅助驾驶已得到广泛应用,其自动刹车的工作原理是用雷达测出车辆与前方障碍物之间的距离(并结合车速转化为所需时间),当此距离等于报警距离时就开始报警提醒,等于危险距离时就自动刹车,某种算法(如下图所示)将报警时间划分为4段,分别为准备时间![]() 、人的反应时间
、人的反应时间![]() 、系统反应时间
、系统反应时间![]() 、制动时间
、制动时间![]() ,相应的距离分别为
,相应的距离分别为![]() 、
、![]() 、
、![]() 、
、![]() ,当车速为
,当车速为![]() (米/秒),且
(米/秒),且![]() 时,通过大数据统计分析得到下表(其中系数
时,通过大数据统计分析得到下表(其中系数![]() 随地面湿滑成都等路面情况而变化,
随地面湿滑成都等路面情况而变化,![]() ).
).
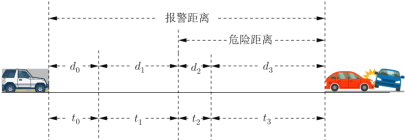
阶段 | 0、准备 | 1、人的反应 | 2、系统反应 | 3、制动 |
时间 |
|
|
|
|
距离 |
|
|
|
|
(1)请写出报警距离![]() (米)与车速
(米)与车速![]() (米/秒)之间的函数关系式
(米/秒)之间的函数关系式![]() ,并求
,并求![]() 时,若汽车达到报警距离时人和系统均不采取任何制动措施,仍以此速度行驶,则汽车撞上固定障碍物的最短时间(精确到0.1秒);
时,若汽车达到报警距离时人和系统均不采取任何制动措施,仍以此速度行驶,则汽车撞上固定障碍物的最短时间(精确到0.1秒);
(2)若要求汽车不论在何种路面情况下行驶,报警距离均小于80米,则汽车的行驶速度应限制在多少米/秒以下?合多少千米/小时?