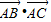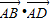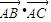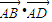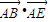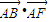题目内容
如图,在边长为a的正方体ABCD-A1B1C1D1中,E是棱AB上一点,M是棱D1C1上一点,则三棱锥M-DEC的体积是
分析:本题中的M,E两点分别是两个线段上的动点,但动中有静,从题设条件与图形可以得出,点M到底面的距离是定值,三角形DEC的面积是定值,故三棱锥M-DEC的体积易求
解答:解:由题意及图,三棱锥M-DEC的高是正方体的棱长为a,三棱锥的底面三角形一边DC=a,又点E到DC的距离是a,故三角形DEC的面积是
a2
由公式,三棱锥M-DEC的体积是
×a×
a2=
a3
故答案为
a3
| 1 |
| 2 |
由公式,三棱锥M-DEC的体积是
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
故答案为
| 1 |
| 6 |
点评:本题考查棱柱、棱锥、棱台的体积,解答本题关键是熟练掌握棱柱的几何性质,且由此性质得出所研究三棱锥的几何性质,依据公式求出它的体积.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
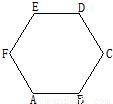
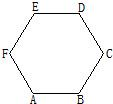
如图,在边长为1的正六边形ABCDEF中,下列向量的数量积中最大的是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
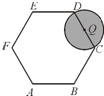 如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量
如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量| AP |
| AB |
| AF |
| A、(1,2] |
| B、[5,6] |
| C、[2,5] |
| D、[3,5] |
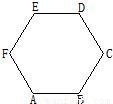
 (2013•资阳模拟)如图,在边长为2的正六边形ABCDEF中,P是△CDE内(含边界)的动点,设向量
(2013•资阳模拟)如图,在边长为2的正六边形ABCDEF中,P是△CDE内(含边界)的动点,设向量