题目内容
已知f(x)是周期为2的奇函数,当x∈(0,1)时,f(x)=2x,则f 值
值
- A.
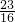
- B.

- C.

- D.

C
分析:先求出-5 <-4,
<-4, ∈(0,1),由f(x)是周期为2的奇函数,可得f
∈(0,1),由f(x)是周期为2的奇函数,可得f  =-f(
=-f( ),根据 当x∈(0,1)时,f(x)=2x ,可求得-f(
),根据 当x∈(0,1)时,f(x)=2x ,可求得-f( ) 的值,从而得到要求的式子的值.
) 的值,从而得到要求的式子的值.
解答:∵ =
= ,
, <
< <
< ,∴-5
,∴-5  <-4,
<-4,
∴-1< <0,且
<0,且  =
= ,故
,故  =
= ∈(0,1).
∈(0,1).
由f(x)是周期为2的奇函数,可得f =f(
=f( )=f (
)=f ( )=-f(-
)=-f(- )=-f(
)=-f( ).
).
∵当x∈(0,1)时,f(x)=2x ,
∴-f( )=-
)=- =-
=-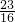 .
.
故 =-f(
=-f( )=-
)=-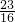 ,
,
故选C.
点评:本题主要考查函数的周期性和奇偶性的综合应用,对数恒等式,体现了转化的数学思想,求得 =-f(
=-f( ),是解题的关键,属于基础题.
),是解题的关键,属于基础题.
分析:先求出-5
 <-4,
<-4, ∈(0,1),由f(x)是周期为2的奇函数,可得f
∈(0,1),由f(x)是周期为2的奇函数,可得f  =-f(
=-f( ),根据 当x∈(0,1)时,f(x)=2x ,可求得-f(
),根据 当x∈(0,1)时,f(x)=2x ,可求得-f( ) 的值,从而得到要求的式子的值.
) 的值,从而得到要求的式子的值.解答:∵
 =
= ,
, <
< <
< ,∴-5
,∴-5  <-4,
<-4,∴-1<
 <0,且
<0,且  =
= ,故
,故  =
= ∈(0,1).
∈(0,1).由f(x)是周期为2的奇函数,可得f
 =f(
=f( )=f (
)=f ( )=-f(-
)=-f(- )=-f(
)=-f( ).
).∵当x∈(0,1)时,f(x)=2x ,
∴-f(
 )=-
)=- =-
=-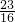 .
.故
 =-f(
=-f( )=-
)=-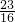 ,
,故选C.
点评:本题主要考查函数的周期性和奇偶性的综合应用,对数恒等式,体现了转化的数学思想,求得
 =-f(
=-f( ),是解题的关键,属于基础题.
),是解题的关键,属于基础题. 
练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx.设a=f(
),b=f(
),c=f(
),则( )
| 6 |
| 5 |
| 3 |
| 2 |
| 5 |
| 2 |
| A、a<b<c |
| B、b<a<c |
| C、c<b<a |
| D、c<a<b |
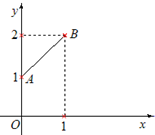 已知f(x)是周期为2的偶函数.当0≤x≤1时,f(x)的图象是如图中的线段AB,那么
已知f(x)是周期为2的偶函数.当0≤x≤1时,f(x)的图象是如图中的线段AB,那么