题目内容
20.在△ABC的边AB、AC上分别取M、N,使$\overrightarrow{AM}=\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{AN}=\frac{1}{3}\overrightarrow{AC}$,BN与CM交于点P,若$\overrightarrow{BP}=λ\overrightarrow{PN}$,$\overrightarrow{PM}=μ\overrightarrow{CP}$,则$\frac{λ}{μ}$=12.分析 画出图形,连接AP,$\overrightarrow{AP}=\overrightarrow{AM}+\overrightarrow{MP}$,根据已知条件及共面向量基本定理即可用$\overrightarrow{AB},\overrightarrow{AC}$来表示$\overrightarrow{AP}$:$\overrightarrow{AP}=\frac{1}{4(μ+1)}\overrightarrow{AB}+\frac{μ}{μ+1}\overrightarrow{AC}$,同理由$\overrightarrow{AP}=\overrightarrow{AN}+\overrightarrow{NP}$又可由$\overrightarrow{AB},\overrightarrow{AC}$表示$\overrightarrow{AP}$:$\overrightarrow{AP}=\frac{λ}{3(λ+1)}\overrightarrow{AC}+\frac{1}{λ+1}\overrightarrow{AB}$,从而由平面向量基本定理即可得到$\left\{\begin{array}{l}{\frac{1}{4(μ+1)}=\frac{1}{λ+1}}\\{\frac{μ}{μ+1}=\frac{λ}{3(λ+1)}}\end{array}\right.$,而两式相除即可求得答案.
解答 解:如图,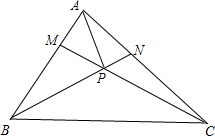 连接AP,根据已知条件,$\overrightarrow{AP}=\overrightarrow{AM}+\overrightarrow{MP}$=$\overrightarrow{AM}-\frac{μ}{μ+1}\overrightarrow{CM}=\overrightarrow{AM}-\frac{μ}{μ+1}$$(\overrightarrow{AM}-\overrightarrow{AC})$=$\frac{1}{4(μ+1)}\overrightarrow{AB}+\frac{μ}{μ+1}\overrightarrow{AC}$;
连接AP,根据已知条件,$\overrightarrow{AP}=\overrightarrow{AM}+\overrightarrow{MP}$=$\overrightarrow{AM}-\frac{μ}{μ+1}\overrightarrow{CM}=\overrightarrow{AM}-\frac{μ}{μ+1}$$(\overrightarrow{AM}-\overrightarrow{AC})$=$\frac{1}{4(μ+1)}\overrightarrow{AB}+\frac{μ}{μ+1}\overrightarrow{AC}$;
同理有$\overrightarrow{AP}=\overrightarrow{AN}+\overrightarrow{NP}=\overrightarrow{AN}-\frac{1}{λ+1}\overrightarrow{BN}$=$\overrightarrow{AN}-\frac{1}{λ+1}(\overrightarrow{AN}-\overrightarrow{AB})$=$\frac{λ}{λ+1}\overrightarrow{AN}+\frac{1}{λ+1}\overrightarrow{AB}$=$\frac{λ}{3(λ+1)}\overrightarrow{AC}+\frac{1}{λ+1}\overrightarrow{AB}$;
根据平面向量基本定理,$\left\{\begin{array}{l}{\frac{1}{4(μ+1)}=\frac{1}{λ+1}}&{①}\\{\frac{μ}{μ+1}=\frac{λ}{3(λ+1)}}&{②}\end{array}\right.$;
$\frac{②}{①}$得,$4μ=\frac{λ}{3}$;
∴$\frac{λ}{μ}=12$.
故答案为:12.
点评 考查向量加法、减法的几何意义及其运算,共面向量基本定理,数乘的几何意义,以及平面向量基本定理.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案(Ⅰ)若要调查该公司使用微信的员工经常使用微信与年龄的关系,列出2×2列联表.
2×2列联表.
| 青年人 | 中年人 | 合计 | |
| 经常使用微信 | |||
| 不经常使用微信 | |||
| 合计 |
(Ⅲ)采用分层抽样的方法从“经常使用微信”中抽取6人,从这6人中任选2人,求事件A“选出的2人均是青年人”的概率.
附:
| P(K2≥k) | 0.010 | 0.001 |
| k | 6.635 | 10.828 |
| A. | x=$\frac{π}{3}$ | B. | x=-$\frac{π}{6}$ | C. | x=-$\frac{π}{24}$ | D. | x=$\frac{11π}{24}$ |
 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°PA=PD=AD=2BC=2,CD=$\sqrt{3},PB=\sqrt{6}$,Q是AD的中点,M是棱PC上的点,且PM=3MC.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°PA=PD=AD=2BC=2,CD=$\sqrt{3},PB=\sqrt{6}$,Q是AD的中点,M是棱PC上的点,且PM=3MC.