题目内容
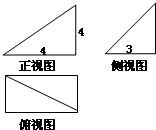
 某几何体的三视图如图,其中俯视图是半个圆,则该几何体的表面积为( )
某几何体的三视图如图,其中俯视图是半个圆,则该几何体的表面积为( )分析:利用三视图判断几何体的形状,通过三视图是数据,求出几何体的表面积即可.
解答:解:由三视图可知几何体底面半径为1,高为
的圆锥的一半,圆锥的母线长为:2.
所以所求几何体的表面积为:S表=S侧+S底=
π•1•1+
×π×1×2+
×2×
=
π+
.
故选C.
| 3 |
所以所求几何体的表面积为:S表=S侧+S底=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
故选C.
点评:本题主要考查关于“几何体的三视图”与“几何体的直观图”的相互转化的掌握情况,同时考查空间想象能力.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 某几何体的三视图如图,它的体积为( )
某几何体的三视图如图,它的体积为( ) (2012•大连二模)某几何体的三视图如图所示,根据图中尺寸(单位:m),可得该几何体的体积为
(2012•大连二模)某几何体的三视图如图所示,根据图中尺寸(单位:m),可得该几何体的体积为 (2012•烟台二模)已知某几何体的三视图如图所示,其中,正视图,侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为
(2012•烟台二模)已知某几何体的三视图如图所示,其中,正视图,侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为 已知某几何体的三视图如图所示,则几何体的体积为( )
已知某几何体的三视图如图所示,则几何体的体积为( )