题目内容
已知圆的方程是x2+y2-2ax+2(a-2)y+2=0,其中a≠1,且a∈R.(1)求证:a取不为1的实数时,上述圆恒过定点;
(2)求与圆相切的直线方程;
(3)求圆心的轨迹方程.
解:(1)将方程x2+y2-2ax+2(a-2)y+2=0整理得 x2+y2-4y+2-a(2x-2y)=0, 令 (2)易得已知圆的圆心坐标为(a,2-a),半径为 设所求切线方程为y=kx+b,即kx-y+b=0. 则圆心到直线的距离应等于圆的半径,即 整理,得2(1+k2)a2-4(1+k2)a+2(1+k2)=(k+1)2a2+2(b-2)(k+1)a+(b-2)2恒成立. 比较系数可得 所以,所求的切线方程是y=x. (3)圆心坐标为(a,2-a),又设圆心坐标为(x,y),则有
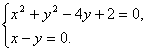 解之得
解之得![]() ∴定点为(1,1).
∴定点为(1,1).![]() |a-1|.
|a-1|.![]() =
=![]() |a-1|恒成立,
|a-1|恒成立,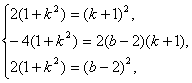 解之得k=1,b=0.2(1+k2)=(b-2)2,
解之得k=1,b=0.2(1+k2)=(b-2)2,![]() 消去参数得x+y=2为所求的圆心的轨迹方程.
消去参数得x+y=2为所求的圆心的轨迹方程. 练习册系列答案
练习册系列答案
西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
萌齐小升初强化模拟训练系列答案
相关题目
已知圆的方程是x2+y2=1,则在y轴上截距为
的切线方程为( )
| 2 |
A、y=x+
| ||||
B、y=-x+
| ||||
C、y=x+
| ||||
D、x=1或y=x+
|