题目内容
12.某地本年度旅游业收人估计为400万元,由于该地出台了一系列措施,进一步发展旅游业.预计今后旅游业的收人每年会比上一年增加$\frac{1}{4}$.(1)求n年内旅游业的总收人;
(2)试估计大约几年后,旅游业的总收入超过8000万元.
分析 (1)根据题意,得出今后每年的旅游业收人组成等比数列,求出前n项和即可;
(2)令前n项和Sn≥8000,求出满足条件的n值即可.
解答 解:(1)根据题意,得;
今后每年的旅游业收人组成等比数列,
且首项为a1=400,公比q=$\frac{5}{4}$,
∴n年内旅游业的总收人为
Sn=$\frac{{a}_{1}(1{-q}^{n})}{1-q}$
=$\frac{400(1{-(\frac{5}{4})}^{n})}{1-\frac{5}{4}}$
=1600[${(\frac{5}{4})}^{n}$-1];
(2)令Sn≥8000,
即1600[${(\frac{5}{4})}^{n}$-1]≥8000,
即${(\frac{5}{4})}^{n}$≥6,
∴n≥${log}_{\frac{5}{4}}$6=$\frac{lg6}{lg\frac{5}{4}}$
=$\frac{lg2+lg3}{lg5-lg4}$
=$\frac{lg2+lg3}{1-3lg2}$
=$\frac{0.301+0.477}{1-3×0.301}$≈8;
∴估计大约8年后,旅游业的总收入超过8000万元.
点评 本题考查了等比数列的通项公式与前n项和公式的应用问题,是基础题目.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
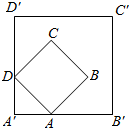 如图所示,边长为1的正方形ABCD的顶点A,D分别在边长为2的正方形A′B′C′D′的边A′B′和A′D′上移动,则$\overrightarrow{A'B}•\overrightarrow{A'C}$的最大值是( )
如图所示,边长为1的正方形ABCD的顶点A,D分别在边长为2的正方形A′B′C′D′的边A′B′和A′D′上移动,则$\overrightarrow{A'B}•\overrightarrow{A'C}$的最大值是( )