题目内容
已知函数
(1)设t=log2x,求t的取值范围;
(2)求f(x)的最值,并给出函数取得最值时相应的x的值.
【答案】分析:(1)由 ,得
,得 ,算出即可;
,算出即可;
(2)把f(x)化为关于t的二次函数,根据二次函数的性质及-2≤t<2即可求得其最值及x取值.
解答:解:(1)∵t=log2x, ,
,
∴ ,
,
∴-2≤t<2,即t的取值范围是[-2,2).
(2)f(x)=log2(4x)•log2(2x)=(log24+log2x)(log22+log2x)
=(2+log2x)(1+log2x)=(2+t)(1+t)
=t2+3t+2= -
- ,
,
∵-2≤t<2,
当 即
即 时,f(x)取得最小值,且
时,f(x)取得最小值,且 .
.
f(x)无最大值.
点评:本题考查对数函数的图象及其性质,考查二次函数最值的求法,属中档题.
 ,得
,得 ,算出即可;
,算出即可;(2)把f(x)化为关于t的二次函数,根据二次函数的性质及-2≤t<2即可求得其最值及x取值.
解答:解:(1)∵t=log2x,
 ,
,∴
 ,
,∴-2≤t<2,即t的取值范围是[-2,2).
(2)f(x)=log2(4x)•log2(2x)=(log24+log2x)(log22+log2x)
=(2+log2x)(1+log2x)=(2+t)(1+t)
=t2+3t+2=
 -
- ,
,∵-2≤t<2,
当
 即
即 时,f(x)取得最小值,且
时,f(x)取得最小值,且 .
.f(x)无最大值.
点评:本题考查对数函数的图象及其性质,考查二次函数最值的求法,属中档题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
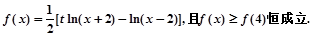
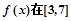 上取得最大值;
上取得最大值;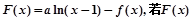 是单调递增函数,求a的取值范围.
是单调递增函数,求a的取值范围.

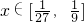 ,求函数f(x)最大值和最小值;
,求函数f(x)最大值和最小值;