题目内容

已知函数 $数学公式$
（1）设log₃x=t，试将f（x）表示成t的函数g（t）；
（2）若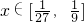 $数学公式$ ，求函数f（x）最大值和最小值；
（3）若方程f（x）+m=0有两根α，β，试求α•β的值．

解：（1）f（x）=（log₃x-3）（log₃x+1）
令log₃x=t，t∈[-3，-2]∴g（t）=t²-2t-3，t∈[-3，-2]
（2）g（t）对称轴t=1
∴f_max（x）=g（-3）=12
f_min（x）=g（-2）=5
（3）即方程（log₃x）²-2log₃x-3+m=0的两解为α，β
∴log₃α+log₃β=2
∴log₃α•β=2
∴α•β=9
分析：（1）利用对数的运算法则商的对数法则及积的对数法则将f（x）用t表示．
（2）由x的范围t的范围，利用二次函数的对称轴公式求出对称轴，利用二次函数的单调性求出二次函数的最值．
（3）利用二次方程根与系数的关系得到α，β满足的等式，求出αβ的值．
点评：本题考查对数函数的运算法则、二次函数最值的求法、二次方程的韦达定理．