题目内容
已知函数![]()
(1)求t的值;
(2)求x为何值时,![]() 上取得最大值;
上取得最大值;
(3)设![]() 是单调递增函数,求a的取值范围.
是单调递增函数,求a的取值范围.
(1)![]() 恒成立,
恒成立,
![]() 的最小值
的最小值
又![]()
(2)由上问知![]()

(3)∵ F(x)是单调递增函数,![]() 恒成立
恒成立
又![]()
显然在![]() 恒成立.
恒成立.
![]() 恒成立.
恒成立.
下面分情况讨论![]() 的解的情况.
的解的情况.
当![]() 时,显然不可能有
时,显然不可能有![]() 上恒成立.
上恒成立.
当![]() 上恒成立.
上恒成立.
当![]() 时,又有两种情况:①
时,又有两种情况:①![]() ;
;
②![]()
由①得![]() ,无解;由②得
,无解;由②得![]()
综上所述各种情况,当![]() 上恒成立.
上恒成立.
∴所求的a的取值范围为![]()

练习册系列答案
相关题目

 的单调递增区间;
的单调递增区间; 中,内角A,B,C的对边分别为
中,内角A,B,C的对边分别为 ,已知
,已知 ,
, 成等差数列,且
成等差数列,且 ,求边
,求边 的值.
的值.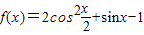
 ,且
,且 ,求sinx的值.
,求sinx的值.
 ,b=1,
,b=1, ,且a>b,试求角B和角C.
,且a>b,试求角B和角C.
 的最小正周期及在区间
的最小正周期及在区间 上的最大值和最小值;
上的最大值和最小值; ,求
,求 的值.
的值.