题目内容
【题目】已知函数f(x)![]() 是R上的奇函数.
是R上的奇函数.
(1)若x∈[![]() ,
,![]() ],求f(x)的取值范围
],求f(x)的取值范围
(2)若对任意的x1∈[1,![]() ,总存在x2∈[
,总存在x2∈[![]() ,
,![]() ]使得mlog2(﹣6x12+24x1﹣16)﹣f(x2)
]使得mlog2(﹣6x12+24x1﹣16)﹣f(x2)![]() 0(m>0)成立,求实数m的取值范围.
0(m>0)成立,求实数m的取值范围.
【答案】(1)[4,5](2)![]() .
.
【解析】
(1)利用奇函数的性质,结合f(0)=0,求得a=2,从而确定出函数的解析式,之后换元,令t=sinx,结合题中所给的自变量的范围,求得![]() ,得到函数
,得到函数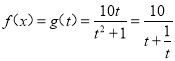 ,利用函数的单调性求得结果;
,利用函数的单调性求得结果;
(2)根据题意,将问题转化为两个函数值域之间的关系,先求出两个函数的值域,之后应用具备包含关系的两个集合的特征,列出对应的不等式组,求得结果.
(1)由题意,f(0)=0,即a﹣2=0,解得a=2,
∴![]() ,令t=sinx,由x∈[
,令t=sinx,由x∈[![]() ,
,![]() ]得,
]得,![]() ,
,
∴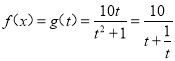 ,
,
易知函数g(t)在![]() 上单调递增,故g(t)∈[4,5],
上单调递增,故g(t)∈[4,5],
∴f(x)的取值范围为[4,5];
(2)由已知,对任意的x1∈[1,![]() ,总存在x2∈[
,总存在x2∈[![]() ,
,![]() ]使得mlog2(﹣6x12+24x1﹣16)
]使得mlog2(﹣6x12+24x1﹣16)![]() f(x2)(m>0)成立,
f(x2)(m>0)成立,
设函数![]() ,的值域为集合A,函数
,的值域为集合A,函数![]() 的值域为集合B,
的值域为集合B,
由已知,AB,由(1)得B=[4,5],
当x1∈[1,![]() 时,
时,![]() ,
,![]() ,
,
故![]() ,
,
则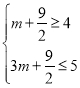 ,
,
解得![]() ,
,
又m>0,故实数m的取值范围为![]() .
.

【题目】某同学为了计算函数![]() 图象与x轴,直线
图象与x轴,直线![]() ,
,![]() 所围成形状A的面积,采用“随机模拟方法”,用计算机分别产生10个在
所围成形状A的面积,采用“随机模拟方法”,用计算机分别产生10个在![]() 上的均匀随机数
上的均匀随机数![]() 和10个在
和10个在![]() 上的均匀随机数
上的均匀随机数![]() ,其数据记录为如下表的前两行.
,其数据记录为如下表的前两行.
| 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
| 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
| 0.92 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
(1)依据表格中的数据回答,在图形A内的点有多少个,分别是什么?
(2)估算图形A的面积.
