题目内容
【题目】已知数列![]() 满足
满足![]() ,且
,且![]() .
.
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)是否存在实数![]() ,
,![]() ,使得
,使得 ,对任意正整数
,对任意正整数![]() 恒成立?若存在,求出实数
恒成立?若存在,求出实数![]() 、
、![]() 的值并证明你的结论;若不存在,请说明理由.
的值并证明你的结论;若不存在,请说明理由.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)存在实数
;(Ⅱ)存在实数![]() ,
,![]() 符合题意.
符合题意.
【解析】
(Ⅰ)由题意可整理为![]() ,从而代入
,从而代入![]() ,即可求
,即可求![]() ,
,![]() 的值;
的值;
(Ⅱ)当![]() 时和
时和![]() 时,可得到一组
时,可得到一组![]() 、
、![]() 的值,于是假设该式成立,用数学归纳法证明即可.
的值,于是假设该式成立,用数学归纳法证明即可.
(Ⅰ)因为![]() ,整理得
,整理得![]() ,
,
由![]() ,代入得
,代入得![]() ,
,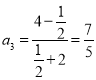 .
.
(Ⅱ)假设存在实数![]() 、
、![]() ,使得
,使得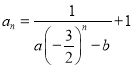 对任意正整数
对任意正整数![]() 恒成立.
恒成立.
当![]() 时,
时,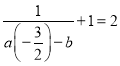 ,①
,①
当![]() 时,
时,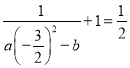 ,②
,②
由①②解得:![]() ,
,![]() .
.
下面用数学归纳法证明:
存在实数![]() ,
,![]() ,使
,使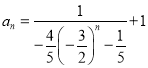 对任意正整数
对任意正整数![]() 恒成立.
恒成立.
(1)当![]() 时,结论显然成立.
时,结论显然成立.
(2)当![]() 时,假设存在
时,假设存在![]() ,
,![]() ,使得
,使得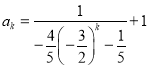 成立,
成立,
那么,当![]() 时,
时,
![]()
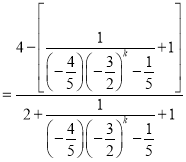
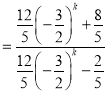
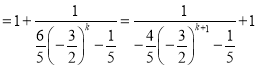 .
.
即当![]() 时,存在
时,存在![]() ,
,![]() ,使得
,使得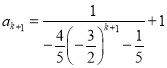 成立.
成立.
由(1)(2)得:
存在实数![]() ,
,![]() ,使
,使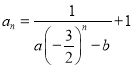 对任意正整数
对任意正整数![]() 恒成立.
恒成立.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目