题目内容
已知一列非零向量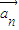 ,n∈N*,满足:
,n∈N*,满足: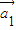 =(10,-5),
=(10,-5),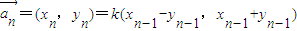 ,(n32 ).,其中k是非零常数.
,(n32 ).,其中k是非零常数.(1)求数列{|
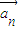 |}是的通项公式;
|}是的通项公式;(2)求向量
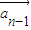 与
与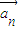 的夹角;(n≥2);
的夹角;(n≥2);(3)当k=
 时,把
时,把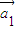 ,
,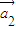 ,…,
,…,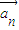 ,…中所有与
,…中所有与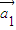 共线的向量按原来的顺序排成一列,记为
共线的向量按原来的顺序排成一列,记为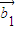 ,
,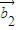 ,…,
,…,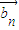 ,…,令
,…,令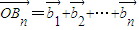 ,O为坐标原点,求点列{Bn}的极限点B的坐标.(注:若点坐标为(tn,sn),且
,O为坐标原点,求点列{Bn}的极限点B的坐标.(注:若点坐标为(tn,sn),且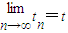 ,
,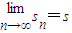 ,则称点B(t,s)为点列的极限点.)
,则称点B(t,s)为点列的极限点.)
【答案】分析:(1)由题意得出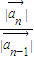 =
=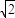 |k|,从而{|
|k|,从而{|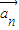 |}是首项为5
|}是首项为5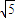 公比为
公比为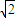 |k|的等比数列.利用等比数列的通项公式即可求得
|k|的等比数列.利用等比数列的通项公式即可求得
数列{|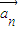 |}是的通项公式;
|}是的通项公式;
(2)由向量的数量积公式得: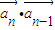 =k(xn-1-yn-1,xn-1+yn-1)•(xn-1,yn-1)=k(xn-12+yn-12)=
=k(xn-1-yn-1,xn-1+yn-1)•(xn-1,yn-1)=k(xn-12+yn-12)=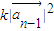 .
.
从而求得cos<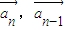 >下面分两种情形:当k>0时,当k<0时,求得向量
>下面分两种情形:当k>0时,当k<0时,求得向量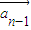 与
与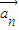 的夹角即可;
的夹角即可;
(3)当k= 时,由(2)知:4<
时,由(2)知:4<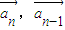 >=p,由于每相隔3个向量的两个向量必共线,且方向相反,得到与向量
>=p,由于每相隔3个向量的两个向量必共线,且方向相反,得到与向量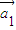 共线的向量,记
共线的向量,记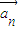 的单位向量为
的单位向量为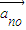 ,利用条件求得
,利用条件求得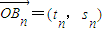 ,最后利用等比数列的求和公式结合数列的极限即可求得点列{Bn}的极限点B的坐标.
,最后利用等比数列的求和公式结合数列的极限即可求得点列{Bn}的极限点B的坐标.
解答:解:(1)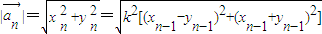 (2分)
(2分)
=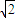 |k|
|k| =
=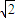 |k||
|k||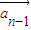 |,(n≥2),
|,(n≥2),
∴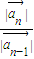 =
=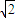 |k|≠0,|
|k|≠0,|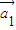 |=5
|=5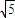 .
.
∴{|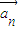 |}是首项为5
|}是首项为5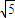 公比为
公比为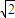 |k|的等比数列.
|k|的等比数列.
∴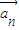 =5
=5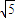 (
(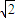 |k|)n-1(2分)
|k|)n-1(2分)
(2)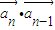 =k(xn-1-yn-1,xn-1+yn-1)•(xn-1,yn-1)
=k(xn-1-yn-1,xn-1+yn-1)•(xn-1,yn-1)
=k(xn-12+yn-12)=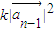 .
.
∴cos<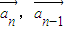 >=
>=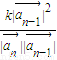 =
=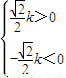 ,(2分)
,(2分)
∴当k>0时,<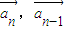 >=
>=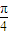 ,
,
当k<0时,<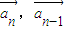 >=
>=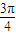 .(2分)
.(2分)
(3)当k= 时,由(2)知:4<
时,由(2)知:4<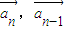 >=p,
>=p,
∴每相隔3个向量的两个向量必共线,且方向相反,
∴与向量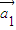 共线的向量为:{
共线的向量为:{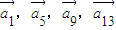 ,}
,}
={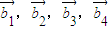 },(2分)
},(2分)
记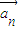 的单位向量为
的单位向量为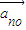 ,则
,则 ,
,
则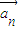 =|
=|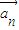 |
|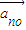 =|a1|(
=|a1|(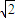 |k|)n-1
|k|)n-1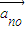
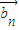 =
=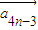 =|a1|(
=|a1|( |k|)4n-4(-1)n-1
|k|)4n-4(-1)n-1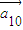
=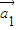 (-4|k|4)n-1=(10,-5)(-
(-4|k|4)n-1=(10,-5)(- )n-1(2分)
)n-1(2分)
设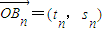 ,
,
则tn=10[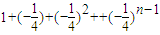 ]=
]=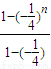 ,
,
∴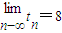 ,
,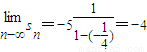 .
.
∴点列{Bn}的极限点B的坐标为(8,-4).(2分)
点评:本小题主要考查等比数列的通项公式、数量积表示两个向量的夹角、数列的极限等基础知识,考查运算求解能力与转化思想.属于基础题.
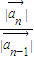 =
=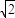 |k|,从而{|
|k|,从而{|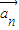 |}是首项为5
|}是首项为5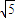 公比为
公比为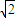 |k|的等比数列.利用等比数列的通项公式即可求得
|k|的等比数列.利用等比数列的通项公式即可求得数列{|
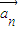 |}是的通项公式;
|}是的通项公式;(2)由向量的数量积公式得:
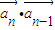 =k(xn-1-yn-1,xn-1+yn-1)•(xn-1,yn-1)=k(xn-12+yn-12)=
=k(xn-1-yn-1,xn-1+yn-1)•(xn-1,yn-1)=k(xn-12+yn-12)=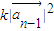 .
.从而求得cos<
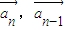 >下面分两种情形:当k>0时,当k<0时,求得向量
>下面分两种情形:当k>0时,当k<0时,求得向量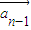 与
与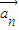 的夹角即可;
的夹角即可;(3)当k=
 时,由(2)知:4<
时,由(2)知:4<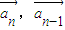 >=p,由于每相隔3个向量的两个向量必共线,且方向相反,得到与向量
>=p,由于每相隔3个向量的两个向量必共线,且方向相反,得到与向量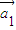 共线的向量,记
共线的向量,记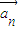 的单位向量为
的单位向量为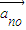 ,利用条件求得
,利用条件求得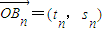 ,最后利用等比数列的求和公式结合数列的极限即可求得点列{Bn}的极限点B的坐标.
,最后利用等比数列的求和公式结合数列的极限即可求得点列{Bn}的极限点B的坐标.解答:解:(1)
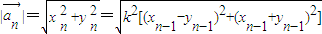 (2分)
(2分)=
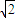 |k|
|k| =
=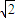 |k||
|k||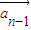 |,(n≥2),
|,(n≥2),∴
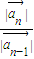 =
=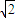 |k|≠0,|
|k|≠0,|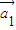 |=5
|=5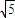 .
.∴{|
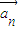 |}是首项为5
|}是首项为5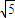 公比为
公比为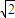 |k|的等比数列.
|k|的等比数列.∴
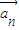 =5
=5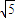 (
(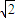 |k|)n-1(2分)
|k|)n-1(2分)(2)
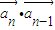 =k(xn-1-yn-1,xn-1+yn-1)•(xn-1,yn-1)
=k(xn-1-yn-1,xn-1+yn-1)•(xn-1,yn-1)=k(xn-12+yn-12)=
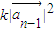 .
.∴cos<
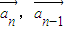 >=
>=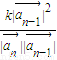 =
=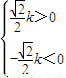 ,(2分)
,(2分)∴当k>0时,<
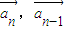 >=
>=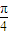 ,
,当k<0时,<
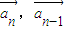 >=
>=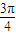 .(2分)
.(2分)(3)当k=
 时,由(2)知:4<
时,由(2)知:4<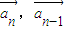 >=p,
>=p,∴每相隔3个向量的两个向量必共线,且方向相反,
∴与向量
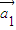 共线的向量为:{
共线的向量为:{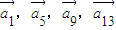 ,}
,}={
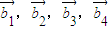 },(2分)
},(2分)记
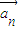 的单位向量为
的单位向量为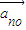 ,则
,则 ,
,则
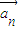 =|
=|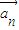 |
|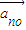 =|a1|(
=|a1|(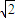 |k|)n-1
|k|)n-1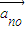
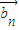 =
=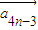 =|a1|(
=|a1|( |k|)4n-4(-1)n-1
|k|)4n-4(-1)n-1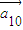
=
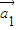 (-4|k|4)n-1=(10,-5)(-
(-4|k|4)n-1=(10,-5)(- )n-1(2分)
)n-1(2分)设
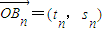 ,
,则tn=10[
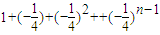 ]=
]=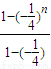 ,
,∴
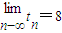 ,
,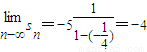 .
.∴点列{Bn}的极限点B的坐标为(8,-4).(2分)
点评:本小题主要考查等比数列的通项公式、数量积表示两个向量的夹角、数列的极限等基础知识,考查运算求解能力与转化思想.属于基础题.

练习册系列答案
相关题目