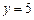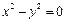题目内容
抛物线y=-x2上的点到直线4x+3y-8=0距离的最小值是( )
A. | B. | C. | D.3 |
A
通过直线4x+3y-8=0平移与抛物线y=-x2相切,设切线为4x+3y+b=0,与y=-x2联立消去y得3x2-4x-b=0,Δ=16+12b=0.
求得 ,所以切线方程为4x+3y
,所以切线方程为4x+3y =0.
=0.
故切点到直线4x+3y-8=0的距离最小值即为两直线间距离,即 .
.
求得
 ,所以切线方程为4x+3y
,所以切线方程为4x+3y =0.
=0.故切点到直线4x+3y-8=0的距离最小值即为两直线间距离,即
 .
.
练习册系列答案
相关题目
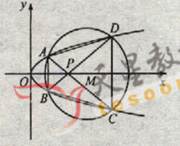 (22) (本小题满分12分)(注意:在试题卷上作答无效)如图,已知抛物线
(22) (本小题满分12分)(注意:在试题卷上作答无效)如图,已知抛物线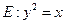
 与圆
与圆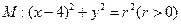 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。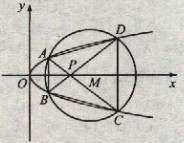
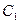 :
: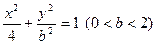 的离心率等于
的离心率等于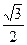 ,抛物线
,抛物线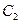 :
: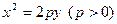 的焦点在椭圆的顶点上。(Ⅰ)求抛物线
的焦点在椭圆的顶点上。(Ⅰ)求抛物线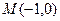 的直线
的直线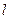 与抛物线
与抛物线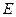 、
、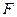 两点,又过
两点,又过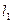 、
、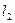 ,当
,当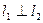 时,求直线
时,求直线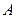 的坐标是
的坐标是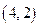 ,底边一个端点
,底边一个端点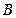 的坐标是
的坐标是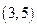 ,求另一个端点
,求另一个端点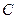 的轨迹方程,并说明它是什么图形.
的轨迹方程,并说明它是什么图形.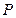 是椭圆
是椭圆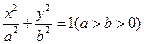 上异于长轴端点的任一点,
上异于长轴端点的任一点,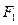 ,
,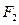 是椭圆的两个焦点,若
是椭圆的两个焦点,若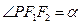 ,
,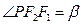 .求证:椭圆的离心率
.求证:椭圆的离心率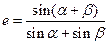 .
.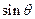 ,
,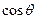 是方程
是方程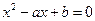 的两根,求点
的两根,求点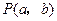 的轨迹方程.
的轨迹方程.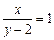 表示斜率为1,在
表示斜率为1,在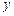 轴上的截距为2的直线
轴上的截距为2的直线 三个顶点的坐标是
三个顶点的坐标是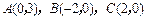 ,中线
,中线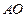 的方程是
的方程是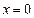
 轴距离为5的点的轨迹方程是
轴距离为5的点的轨迹方程是