题目内容

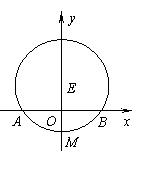
如图所示,已知圆交x轴分别于A,B两点,交y轴的负半轴于点M,过点M作圆E的弦MN．

（1）若弦MN所在直线的斜率为2,求弦MN的长；

（2）若弦MN的中点恰好落在x轴上,求弦MN所在直线的方程；

（3）设弦MN上一点P(不含端点)满足成等比数列(其中O为坐标原点),试探求的取值范围．

             

解：（1）在圆E的方程中令x=0,得M(0,－1),又,所以弦MN所在直线的方程为,即．

∵圆心到直线MN的距离为,且,∴．

（2）因为,所以,代入圆E的方程中得．      

由M(0,－1), 得直线MN的方程为或．

易得,设,

则由,得,

化简得    ①

由题意知点P在圆E内,所以,结合①,得,解得．从而=．

练习册系列答案
相关题目
如图所示，已知圆M：（x+1）2+y2=8及定点N（1，0），点P是圆M上一动点，点Q为PN的中点，PM上一点G满足
GQ
•
NP
=0
（1）求点G的轨迹C的方程；
（2）已知直线l：y=kx+m与曲线C交于A、B两点，E（0，1），是否存在直线l，使得点N恰为△ABE的垂心？若存在，求出直线l的方程，若不存在，请说明理由．
（理）如图所示，已知圆C：（x+1）2+y2=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足
AM
=2
AP
，
NP
•
AM
=0，点N的轨迹为曲线E．
（1）求曲线E的方程；
（2）过点S（0，
1
3
）且斜率为k的动直线l交曲线E于A、B两点，在y轴上是否存在定点G，满足
GP
=
GA
+
GB
使四边形NAPB为矩形？若存在，求出G的坐标和四边形NAPB面积的最大值；若不存在，说明理由．
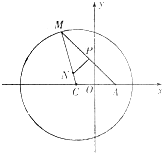精英家教网如图所示，已知圆C：（x+1）2+y2=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足AM=2AP，NP⊥AM，点N的轨迹为曲线E．
（1）求曲线E的方程；
（2）若过定点F（0，2）的直线l交曲线E于不同的两点G、H（点G在点F、H之间），且满足FG=
1
2
FH，求直线l的方程；
（3）设曲线E的左右焦点为F1，F2，过F1的直线交曲线于Q，S两点，过F2的直线交曲线于R，T两点，且QS⊥RT，垂足为W；
（ⅰ）设W（x0，y0），证明：
x
2
0
2
+
y
2
0
＜1；
（ⅱ）求四边形QRST的面积的最小值．
（2006•石景山区一模）如图所示，已知圆C：（x+1）2+y2=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足
AM
=2
AP
，
NP
•
AM
=0，点N的轨迹为曲线E．
（Ⅰ） 求曲线E的方程；
（Ⅱ） 若点B1（x1，y1），B2（-1，y2），B3（x3，y3）在曲线E上，线段B1B3的垂直平分线为直线l，且|B1A|，|B2A|，|B3A|成等差数列，求x1+x3的值，并证明直线l过定点；
（Ⅲ）若过定点F（0，2）的直线交曲线E于不同的两点G、H（点G在点F、H之间），且满足
FG
=λ
FH
，求λ的取值范围．
如图所示，已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点，点P在AM上，点N在CM上，且满足=2,·=0,点N的轨迹为曲线E.

(1)求曲线E的方程；

(2)过点A且倾斜角是45°的直线l交曲线E于两点H、Q，求|HQ|.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网