题目内容
数列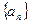 的各项均为正值,
的各项均为正值,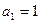 ,对任意
,对任意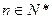 ,
,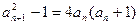 ,
,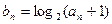 都成立.
都成立.
求数列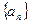 、
、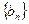 的通项公式;
的通项公式;
当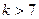 且
且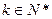 时,证明对任意
时,证明对任意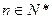 都有
都有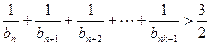 成立.
成立.
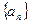 的各项均为正值,
的各项均为正值,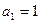 ,对任意
,对任意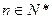 ,
,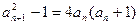 ,
,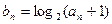 都成立.
都成立.求数列
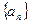 、
、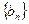 的通项公式;
的通项公式;当
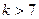 且
且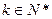 时,证明对任意
时,证明对任意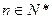 都有
都有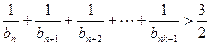 成立.
成立.(1) 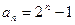
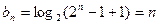 (2)同解析
(2)同解析
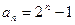
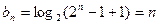 (2)同解析
(2)同解析解:由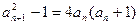 得,
得,
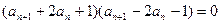
数列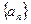 的各项为正值,
的各项为正值,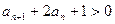
∴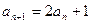
∴
又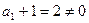
∴数列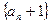 为等比数列.
为等比数列.
∴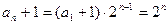 ,
, 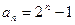 ,即为数列
,即为数列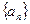 的通项公式.
的通项公式.
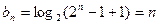
(2)设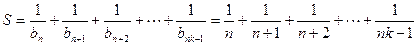
∴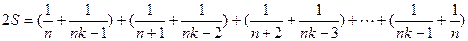 (1)
(1)
当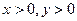 时,
时,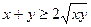 ,
,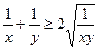
∴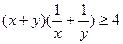
∴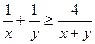 , 当且仅当
, 当且仅当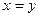 时等号成立.
时等号成立.
上述(1)式中,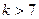 ,
,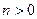 ,
,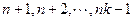 全为正,所以
全为正,所以
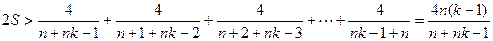
∴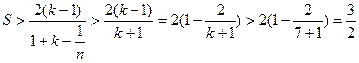 得证.
得证.
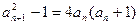 得,
得,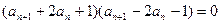
数列
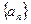 的各项为正值,
的各项为正值,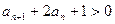
∴
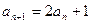
∴

又
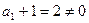
∴数列
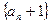 为等比数列.
为等比数列. ∴
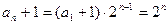 ,
, 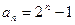 ,即为数列
,即为数列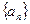 的通项公式.
的通项公式. 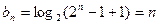
(2)设
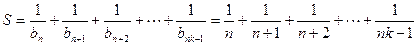
∴
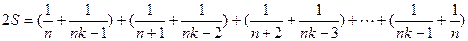 (1)
(1) 当
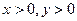 时,
时,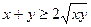 ,
,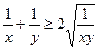
∴
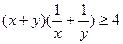
∴
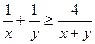 , 当且仅当
, 当且仅当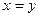 时等号成立.
时等号成立. 上述(1)式中,
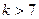 ,
,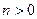 ,
,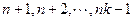 全为正,所以
全为正,所以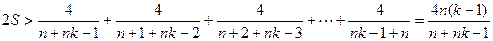
∴
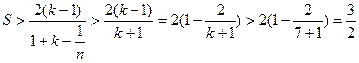 得证.
得证.
练习册系列答案
相关题目
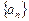 中,其中
中,其中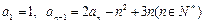
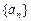 的通项公式;
的通项公式;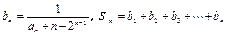 ,证明:当
,证明:当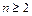 时,
时,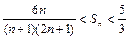 .
. (x≥4)的反函数为
(x≥4)的反函数为 ,数列
,数列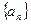 满足:a1=1,
满足:a1=1, ,(
,( N*),数列
N*),数列 ,
, ,
, ,…,
,…, 是首项为1,公比为
是首项为1,公比为 的等比数列.
的等比数列. ,求数列
,求数列 的前n项和
的前n项和 .
.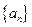 中,
中,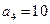 且
且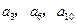 成等比数列.
成等比数列.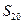 .
.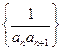 前n项的和
前n项的和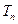 .
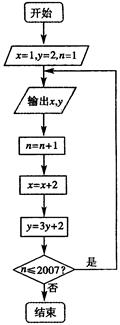
.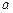 的值依次分别记为
的值依次分别记为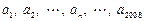 ,将输出的
,将输出的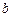 的值依次分别记为
的值依次分别记为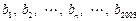 .
.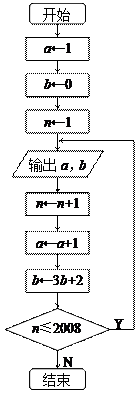
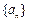 ,
,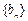 通项公式;
通项公式;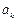 与
与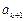 中插入
中插入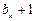 个3,就能得到一个新数列
个3,就能得到一个新数列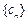 ,则
,则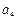 是数列
是数列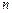 项和为
项和为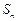 ,问是否存在这样的正整数
,问是否存在这样的正整数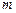 ,使数列
,使数列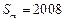 ,如果存在,求出
,如果存在,求出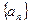 的各项均为正数,它的前n项和Sn满足
的各项均为正数,它的前n项和Sn满足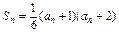 ,并且
,并且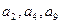 成等比数列.
成等比数列. 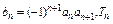 为数列
为数列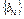 的前n项和,求
的前n项和,求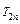 .
.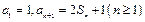
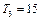 ,又
,又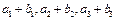 成等比数列,求Tn
成等比数列,求Tn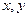 值依
值依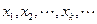 ;
;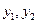 ,…,
,…,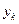 ,….
,….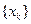 和
和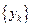 的通项公式;
的通项公式;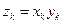 ,求数列
,求数列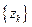 的前
的前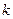 项和
项和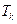 ,
, 其中
其中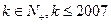 .
.