题目内容
4.已知在等比数列{an}中,an+1>an,对n∈N*恒成立,且a1a4=8,a2+a3=6.(Ⅰ)求数列{an}的通项公式(
Ⅱ)若数列{bn}满足$\frac{{a}_{1}}{{b}_{1}}+\frac{3{a}_{2}}{{b}_{2}}$+…+$\frac{(2n-1){a}_{n}}{{b}_{n}}$=n,(n∈N*),求数列{bn}的前n项和Sn.
分析 (I)利用等比数列的通项公式及其性质即可得出.
(II)利用等比数列的前n项和公式、“错位相减法”即可得出.
解答 解:(I)设等比数列{an}的公比为q,an+1>an,对n∈N*恒成立,且a1a4=8,a2+a3=6.
∴a2a3=8,联立解得a2=2,a3=4.
∴q=2.
∴an=2×2n-2=2n-1.
(II)∵数列{bn}满足$\frac{{a}_{1}}{{b}_{1}}+\frac{3{a}_{2}}{{b}_{2}}$+…+$\frac{(2n-1){a}_{n}}{{b}_{n}}$=n,(n∈N*),
∴$\frac{{a}_{1}}{{b}_{1}}$=1,解得b1=1.
n≥2时,$\frac{(2n-1){a}_{n}}{{b}_{n}}$=n-(n-1)=1,
∴bn=(2n-1)•2n-1.
∴数列{bn}的前n项和Sn=1+3×2+5×22+…+(2n-1)•2n-1.
2Sn=2+3×22+…+(2n-3)•2n-1+(2n-1)•2n,
∴-Sn=1+2(2+22+…+2n-1)-(2n-1)•2n=$2×\frac{{2}^{n}-1}{2-1}$-1-(2n-1)•2n=(3-2n)•2n-3,
∴Sn=(2n-3)•2n+3.
点评 本题考查了递推关系、等比数列的通项公式及其前n项和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.在△ABC中,知cosA=$\frac{c}{a}$cosC,b+c=2+$\sqrt{2}$,cosB=$\frac{3}{4}$,则△ABC的面积是$\frac{\sqrt{7}}{2}$.
15.函数y=x+lnx2的大致图象为( )
| A. |  | B. |  | ||
| C. |  | D. |  |
13.下列命题的逆命题为真命题的是( )
| A. | 若x>2,则(x-2)(x+1)>0 | B. | 若x2+y2≥4,则xy=2 | ||
| C. | 若x+y=2,则xy≤l | D. | 若a≥b,则ac2≥bc2 |
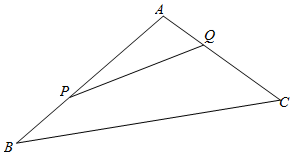 如图,上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区.已知∠A=120°,AB、AC的长度均大于200米.设AP=x,AQ=y,且AP,AQ总长度为200米.
如图,上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区.已知∠A=120°,AB、AC的长度均大于200米.设AP=x,AQ=y,且AP,AQ总长度为200米.