题目内容
如图所示,正方体ABCD—A1B1C1D1中,E、F分别是AB和AA1的中点.
求证:(1)E,C,D1,F四点共面;
(2)CE,D1F,DA三线共点.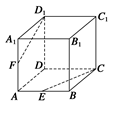
求证:(1)E,C,D1,F四点共面;
(2)CE,D1F,DA三线共点.

证明略
(1)如图所示,连接CD1,EF,A1B,

∵E、F分别是AB和AA1的中点,
∴EF∥A1B且EF= A1B,
A1B,
又∵A1D1 BC,
BC,
∴四边形A1BCD1是平行四边形,∴A1B∥CD1,∴EF∥CD1,
∴EF与CD1确定一个平面 ,
,
∴E,F,C,D1∈ ,
,
即E,C,D1,F四点共面.
(2)由(1)知EF∥CD1,且EF= CD1,
CD1,
∴四边形CD1FE是梯形,
∴CE与D1F必相交,设交点为P,
则P∈CE 平面ABCD,
平面ABCD,
且P∈D1F 平面A1ADD1,
平面A1ADD1,
∴P∈平面ABCD且P∈平面A1ADD1.
又平面ABCD∩平面A1ADD1=AD,
∴P∈AD,∴CE,D1F,DA三线共点.

∵E、F分别是AB和AA1的中点,
∴EF∥A1B且EF=
 A1B,
A1B,又∵A1D1
 BC,
BC,∴四边形A1BCD1是平行四边形,∴A1B∥CD1,∴EF∥CD1,
∴EF与CD1确定一个平面
 ,
,∴E,F,C,D1∈
 ,
,即E,C,D1,F四点共面.
(2)由(1)知EF∥CD1,且EF=
 CD1,
CD1,∴四边形CD1FE是梯形,
∴CE与D1F必相交,设交点为P,
则P∈CE
 平面ABCD,
平面ABCD,且P∈D1F
 平面A1ADD1,
平面A1ADD1,∴P∈平面ABCD且P∈平面A1ADD1.
又平面ABCD∩平面A1ADD1=AD,
∴P∈AD,∴CE,D1F,DA三线共点.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 相交,P为直线AB外的一点,且P不在
相交,P为直线AB外的一点,且P不在
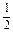 AD,BE
AD,BE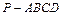 中,
中,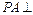 底面
底面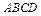 ,
,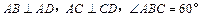 ,
,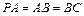 ,
,  是
是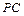 的中点.
的中点.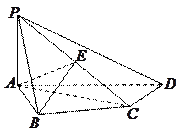 (1)证明
(1)证明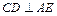 ;
;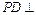 平面
平面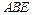 ;
;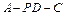 的大小.
的大小.