题目内容
已知函数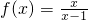 .
.
(Ⅰ)证明:对于定义域中任意的x均有f(1+x)+f(1-x)=2;
(Ⅱ)用函数单调性的定义证明函数f(x)在(1,+∞)上是减函数.
证明:(Ⅰ) =
= ,
,
即对于定义域中任意的x均有f(1+x)+f(1-x)=2.
(Ⅱ)设x1,x2是(1,+∞)上的两个任意实数,且x1<x2,
 =
= .
.
因为1<x1<x2,所以x1-1>0,x2-1>0,x1-x2<0,
所以f(x2)-f(x1)<0,即f(x2)<f(x1),
所以f(x)在(0,+∞)上是减函数.
分析:(1)将f(1+x)和f(1-x)代入进行化简;
(2)要求用定义证明,所以按步骤:取值-作差-化简-判号-结论证明即可.
点评:本题考察函数的性质,属基础题,题目比较常规,所以按常规思路解决就很好.
 =
= ,
,即对于定义域中任意的x均有f(1+x)+f(1-x)=2.
(Ⅱ)设x1,x2是(1,+∞)上的两个任意实数,且x1<x2,
 =
= .
.因为1<x1<x2,所以x1-1>0,x2-1>0,x1-x2<0,
所以f(x2)-f(x1)<0,即f(x2)<f(x1),
所以f(x)在(0,+∞)上是减函数.
分析:(1)将f(1+x)和f(1-x)代入进行化简;
(2)要求用定义证明,所以按步骤:取值-作差-化简-判号-结论证明即可.
点评:本题考察函数的性质,属基础题,题目比较常规,所以按常规思路解决就很好.

练习册系列答案
相关题目

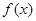 )在区间
)在区间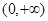 的单调性;
的单调性;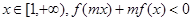 恒成立,求实数
恒成立,求实数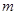 的取值范围。
的取值范围。 ,
, ;
; 是奇函数;
是奇函数; 和
和 的值,由此概括出涉及函数
的值,由此概括出涉及函数 的对所有不等于零的实数
的对所有不等于零的实数 都成立的一个等式,并加以证明
都成立的一个等式,并加以证明 .
. 上是单调函数;
上是单调函数; 上的最值.
上的最值.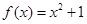
 上是单调递增的。
上是单调递增的。