题目内容
【题目】已知a是实常数，函数
．
（1）若曲线
在
处的切线过点A（0，﹣2），求实数a的值；
（2）若
有两个极值点
（
），
①求证：
；
②求证：
．
【答案】（1）证明详见解析；（2）证明详见解析.
【解析】
试题本题考查导数的运用：求切线方程和单调区间、极值，主要考查导数的几何意义和分类讨论的思想方法，注意函数的单调性的运用，属于中档题．第一问，求出
的导数，求得切线的斜率和切点，由点斜式方程可得切线方程，代入点（0，﹣2），即可解得a；第二问，①依题意：
有两个不等实根
（
），设
，求出导数，讨论当a≥0时，当a＜0时，求得函数g（x）的单调性，令极大值大于0，解不等式即可得证；②由①知：，
变化，求得的增区间，通过导数，判断
，设
（0＜x＜1），求得h（x）的单调性，即可得证．
试题解析：（1）由已知可得，
（x＞0），切点
，
在x=1处的切线斜率为
，
切线方程：
，
把
代入得：a=1；
（2）证明：①依题意：有两个不等实根（），
设则：
（x＞0）
当a≥0时，有
，所以
是增函数，不符合题意；
当a＜0时：由
得：
，
列表如下：
依题意：
，解得：
，
综上可得，得证；
②由①知：，变化如下：
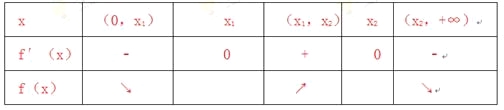
由表可知：在[x1，x2]上为增函数，所以：
又
，故，
由（1）知：
，
（
）
设（
），则
成立，所以
单调递减，
故：
，也就是
,
综上所证：
成立．
练习册系列答案
名校课堂系列答案
相关题目
