题目内容

解析:(1)在第3行中,由左向右的数字依次是:a 1 = 6,a 2 = 9 = a 1 + 3,
a 3 = 13 = a 2 + 4,a 4 = 18 = a 3 + 5,…,归纳可证得:a n = a n 1 + ( n + 1 ),
∴ a 8 = a 7 + 9 = a 6 + 8 + 9 = … = a 4 + 6 + 7 + 8 + 9 = 18 + 30 = 48;
(2)为求数字321在哪个方格内,可将棋盘上的数字按从右上到左下的对角线方向排列如下:第1组 1;第2组 2,3;第3组 4,5,6;第4组 7,8,9,10;……,显然,
从第1组到第n组共包含1 + 2 + 3 + … + n =![]() 个数字,故第n组中最大数字是
个数字,故第n组中最大数字是![]() 。∵ 321是第321个数字,∴ 321所在“组”的行号是满足:
。∵ 321是第321个数字,∴ 321所在“组”的行号是满足:![]() ≥ 321的最小自然数n。试算,从
≥ 321的最小自然数n。试算,从![]() = 300和
= 300和![]() = 325,可得n = 25。第25组中最小的数是数列 1,2,4,7,11,…,(即a n = a n 1 + ( n 1 ))中的第25个数,记为a 25。易知a 25 = a 24 + 24 = a 23 + 23 + 24 = … = a 1 + 1 + 2 + 3 + … + 24 = 301,因而321是第25组中第(321 301 + 1 )个数,即第21个数。∴ 321位于第21行、第5列的方格内;
= 325,可得n = 25。第25组中最小的数是数列 1,2,4,7,11,…,(即a n = a n 1 + ( n 1 ))中的第25个数,记为a 25。易知a 25 = a 24 + 24 = a 23 + 23 + 24 = … = a 1 + 1 + 2 + 3 + … + 24 = 301,因而321是第25组中第(321 301 + 1 )个数,即第21个数。∴ 321位于第21行、第5列的方格内;
(3)位于从左上角到右下角的对角线上的方格内的数字组成的数列是 1,5,13,25,…不妨依次记为b 1,b 2,b 3,…,易见,b n是依(2)中排法的第2 n 1组的中间一个数,即第n个数,∴ b n =![]() ( n 1 ) = 2 n ( n 1 ) + 1 = 2 n 2 2 n + 1,n = 1,2,3,…;
( n 1 ) = 2 n ( n 1 ) + 1 = 2 n 2 2 n + 1,n = 1,2,3,…;
(4)利用自然数平方和的公式:1 2 + 2 2 + 3 2 + … + n 2 =![]() ,可以计算得S n =
,可以计算得S n =![]()
=![]() 2 k 2 2 k + 1 ) = 2
2 k 2 2 k + 1 ) = 2![]() 2 2
2 2![]() + n = 2 ×
+ n = 2 ×![]() 2 ×
2 ×![]() + n =
+ n =![]() 。
。

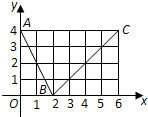 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=