题目内容

四棱锥P-ABCD的底面ABCD是平行四边形，
AB
=（-1，2，1），
AD
=（0，-2，3），
AP
═（8，3，2），
（1）求证：PA⊥底面ABCD；
（2）求PC的长．
证明：（1）∵
AB
=（-1，2，1），
AD
=（0，-2，3），
AP
═（8，3，2），
∴
AP
•
AB
=0，
AP
•
AD
=0，
∴
AP
⊥
AB
，
AP
⊥
AD
，
即AP⊥AB且AP⊥AD，
又∵AB∩AD=A
∴AP⊥平面ABCD；
（2）∵
AB
=（-1，2，1），
AD
=（0，-2，3），
AP
═（8，3，2），
∴
AC
=
AB
+
AD
=(-1，0，4)，
PC
=
AP
-
AC
=(9，3，-2)，
∴|PC|=
94
．
练习册系列答案
相关题目
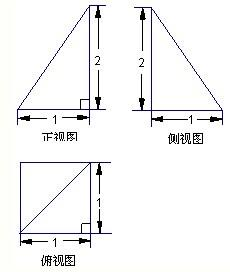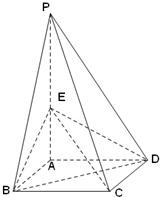精英家教网如图，四棱锥P-ABCD的底面是边长为1的正方形，侧棱PA⊥底面ABCD，且PA=2，E是PA的中点．
（Ⅰ）求四棱锥P-ABCD的体积；
（Ⅱ）求证：PC∥平面BDE．
精英家教网如图所示，四棱锥P-ABCD的底面是边长为a的正方形，侧棱PA⊥底面ABCD，侧面PBC内有BE⊥PC于E，且BE=
6
3
a，试在AB上找一点F，使EF∥平面PAD．
如图，ABCD是正方形，O是该正方形的中心，P是平面ABCD外一点，PO⊥底面ABCD，E是PC的中点．求证：
（1）PA∥平面BDE；
（2）平面EBD⊥平面PAC；
（3）若PA=AB=4，求四棱锥P-ABCD的全面积．
正四棱锥P-ABCD的高为PO，若Q为CD中点，且
OQ
=
PQ
+x
PC
+y
PA
(x，y∈R)则x+y=
-1
-1
．
精英家教网已知四棱锥P-ABCD的三视图如图所示，则这个四棱锥的体积为（　　）
A、
1
3
B、1
C、
2
3
D、
4
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网