题目内容
解：∵
，
∴log5（x+1）+log5（x-3）=log55，
∴（x+1）•（x-3）=5，其中，x+1＞0且x-3＞0
解得x=4．
故方程的解是4
分析：利用对数的运算性质可脱去对数符号，转化为关于x的方程即可求得答案．
点评：本题考查对数的运算性质，考查方程思想，属于基础题．
，∴log5（x+1）+log5（x-3）=log55，
∴（x+1）•（x-3）=5，其中，x+1＞0且x-3＞0
解得x=4．
故方程的解是4
分析：利用对数的运算性质可脱去对数符号，转化为关于x的方程即可求得答案．
点评：本题考查对数的运算性质，考查方程思想，属于基础题．
练习册系列答案
相关题目
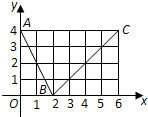如图，函数f（x）的图象是折线段ABC，其中A，B，C的坐标分别为（0，4），（2，0），（6，4），则f（f（0））=