题目内容
函数f(x)=xlnx的减区间是 .
【答案】分析:先求定义域,再令导数≤0解不等式,取交集可得.
解答:解:由题意函数的定义域为(0,+∞),
求导数可得f′(x)=x′lnx+x(lnx)′
=1+lnx,令f′(x)=1+lnx≤0,
解之可得x≤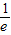
故函数的减区间为: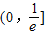
故答案为: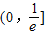
点评:本题考查导数法研究函数的单调性,注意定义域是解决问题的关键,属中档题.
解答:解:由题意函数的定义域为(0,+∞),
求导数可得f′(x)=x′lnx+x(lnx)′
=1+lnx,令f′(x)=1+lnx≤0,
解之可得x≤
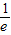
故函数的减区间为:
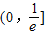
故答案为:
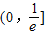
点评:本题考查导数法研究函数的单调性,注意定义域是解决问题的关键,属中档题.

练习册系列答案
相关题目
函数f(x)=xln|x|的图象大致是( )
A、 | B、 | C、 | D、 |