题目内容
(本小题满分12分).已知圆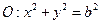 与直线
与直线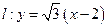 相切。
相切。
(1)求以圆O与y轴的交点为顶点,直线在x轴上的截距为半长轴长的椭圆C方程;
(2)已知点A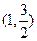 ,若直线与椭圆C有两个不同的交点E,F,且直线AE的斜率与直线
,若直线与椭圆C有两个不同的交点E,F,且直线AE的斜率与直线
AF的斜率互为相反数;问直线的斜率是否为定值?若是求出这个定值;若不是,请说明理由.
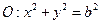 与直线
与直线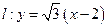 相切。
相切。(1)求以圆O与y轴的交点为顶点,直线在x轴上的截距为半长轴长的椭圆C方程;
(2)已知点A
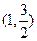 ,若直线与椭圆C有两个不同的交点E,F,且直线AE的斜率与直线
,若直线与椭圆C有两个不同的交点E,F,且直线AE的斜率与直线AF的斜率互为相反数;问直线的斜率是否为定值?若是求出这个定值;若不是,请说明理由.
解:(1) 因为直线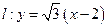 在x轴上的截距为2,所以
在x轴上的截距为2,所以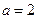
直线的方程变为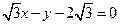 ,由直线与圆相切得
,由直线与圆相切得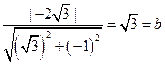
所以椭圆方程为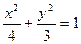
(2)设直线AE方程为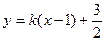 ,
,
代入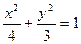 得:
得: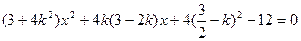
设E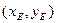 ,F
,F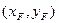 ,因为点A
,因为点A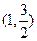 在椭圆上,
在椭圆上,
所以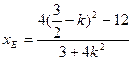 ,
,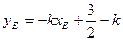
又直线AF的斜率与AE的 斜率互为相反数,
斜率互为相反数,
同理可得: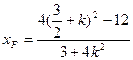 ,
,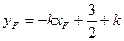 所以直线EF的斜率为
所以直线EF的斜率为
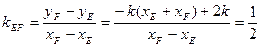
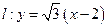 在x轴上的截距为2,所以
在x轴上的截距为2,所以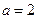
直线的方程变为
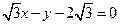 ,由直线与圆相切得
,由直线与圆相切得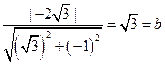
所以椭圆方程为
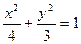
(2)设直线AE方程为
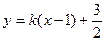 ,
, 代入
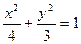 得:
得: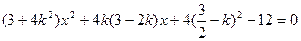
设E
 ,F
,F ,因为点A
,因为点A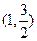 在椭圆上,
在椭圆上,所以
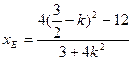 ,
,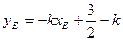
又直线AF的斜率与AE的
 斜率互为相反数,
斜率互为相反数,同理可得:
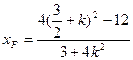 ,
,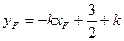 所以直线EF的斜率为
所以直线EF的斜率为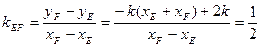
略

练习册系列答案
相关题目
 的直线被圆
的直线被圆 所截得的弦长为
所截得的弦长为



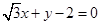 截圆
截圆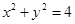 得到的弦长为
得到的弦长为

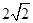
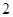
 轨迹方程
轨迹方程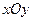 中,以
中,以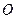 为圆心的圆与直线
为圆心的圆与直线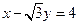 相切.
相切.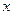 轴相交于
轴相交于
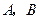 两点,圆内的动点
两点,圆内的动点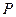 使
使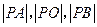 成等比数列,求
成等比数列,求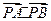 的取值范围(结果用区间表示).:
的取值范围(结果用区间表示).: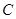 与直线
与直线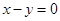 及
及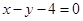 都相切,圆心在直线
都相切,圆心在直线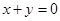 上,则圆
上,则圆



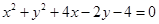 ,则
,则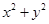 的最大值是 ;
的最大值是 ;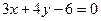 被圆
被圆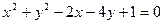 截得的弦长为 .
截得的弦长为 .