题目内容
设二次函数f(x)=a x2-2ax+c在区间[0,1]上单调递减,且f(m)≤f(0),则实数m的取值范围是 ( )
x2-2ax+c在区间[0,1]上单调递减,且f(m)≤f(0),则实数m的取值范围是 ( )
A.(-∞,0] B.[2,+∞) C.[0,2] D.(-∞,0]∪[2,+∞)
C 二次函数f(x)=ax2-2ax+c在区间[0,1]上单调递减,则a≠0,f′(x)=2a(x- 1)<0,x∈[0,1],所以a>0,即函数图象的开口向上,对称轴是直线x=1.所以f(0)
1)<0,x∈[0,1],所以a>0,即函数图象的开口向上,对称轴是直线x=1.所以f(0) =f(2),则当f(
=f(2),则当f( m)≤f(0)时,有0≤m≤2.
m)≤f(0)时,有0≤m≤2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).
(1)求证:f(x)是奇函数;
(2)如果x为正实数,f(x)<0,并且f(1)=-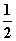 ,试求f(x)在区间[-2,6]上的最值.
,试求f(x)在区间[-2,6]上的最值.
已知 与
与 之间的一组数据如右图所示,则
之间的一组数据如右图所示,则 与
与 的回归直线方程
的回归直线方程 必过定点 .
必过定点 .
|
| 0 | 1 | 2 | 3 |
|
| 1 | 3 | 5-a | 7+a |
 的最小正周期为
的最小正周期为 ,则该函数的图象( )
,则该函数的图象( ) 对称 B.关于直线
对称 B.关于直线 对称
对称 对称 D.关于直线
对称 D.关于直线 对称
对称 是实数,则
是实数,则 的值为( )
的值为( ) B.3 C.0
B.3 C.0  D.
D.
 为实数,
为实数, .
. ,求
,求 在
在 上的最大值和最小值;
上的最大值和最小值; 和
和 上都是递增的,求
上都是递增的,求 =lg x,则f(21)=___________________.
=lg x,则f(21)=___________________. 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足 .
.  ,
, ,求
,求 的长.
的长.