题目内容
偶函数y=f(x)当x∈[0,+∞)时,f(x)=x-1,则f(x-1)<0的解集是 .
【答案】分析:根据函数f(x)是偶函数,且给出了x∈[0,+∞)时的解析式,得到函数y=f(x-1)的图象,由图象可得不等式f(x-1)<0的解集.
解答:解:因为函数y=f(x)是偶函数,且当x∈[0,+∞)时,f(x)=x-1,
所以函数y=f(x-1)的图象如图,
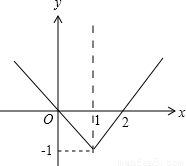
则满足f(x-1)<0的解集是{x|0<x<2}.
故答案为{x|0<x<2}.
点评:本题考查了函数的性质,考查了函数的图象平移,训练了由图象求得不等式的解集,是基础题.
解答:解:因为函数y=f(x)是偶函数,且当x∈[0,+∞)时,f(x)=x-1,
所以函数y=f(x-1)的图象如图,

则满足f(x-1)<0的解集是{x|0<x<2}.
故答案为{x|0<x<2}.
点评:本题考查了函数的性质,考查了函数的图象平移,训练了由图象求得不等式的解集,是基础题.

练习册系列答案
相关题目