题目内容
已知m,n为正整数。
(1)用数学归纳法证明:当x>-1时,(1+x)m≥1+mx;
(2)对于n≥6,已知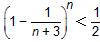 ,求证:
,求证: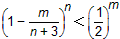 ,m=1,2…,n;
,m=1,2…,n;
(3)求出满足等式3n+4n+…+(n+2)n=(n+3)n的所有正整数n。
(1)用数学归纳法证明:当x>-1时,(1+x)m≥1+mx;
(2)对于n≥6,已知
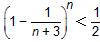 ,求证:
,求证: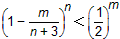 ,m=1,2…,n;
,m=1,2…,n;(3)求出满足等式3n+4n+…+(n+2)n=(n+3)n的所有正整数n。
解:(1)用数学归纳法证明:
(i)当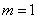 时,原不等式成立;
时,原不等式成立;
当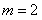 时,左边
时,左边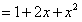 ,右边
,右边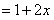 ,
,
因为 ,
,
所以左边≥右边,原不等式成立;
(ii)假设当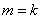 时,不等式成立,即
时,不等式成立,即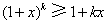 ,
,
则当 时,
时,
∵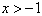 ,
,
∴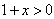 ,
,
于是在不等式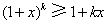 两边同乘以
两边同乘以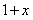 得,
得,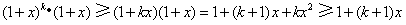
所以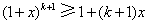
即当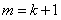 时,不等式也成立
时,不等式也成立
综合(i)(ii)知,对一切正整数,不等式都成立。
(2)当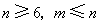 时,由(1)得
时,由(1)得
于是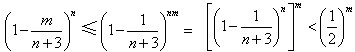 ,
,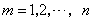 。
。
(3)解:由(2),当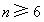 时,
时,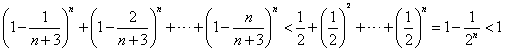 ,
,
∴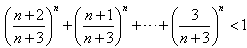
即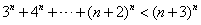
即当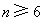 时,不存在满足该等式的正整数n
时,不存在满足该等式的正整数n
故只需要讨论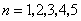 的情形:
的情形:
当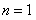 时,
时,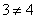 ,等式不成立;
,等式不成立;
当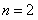 时,
时,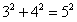 ,等式成立;
,等式成立;
当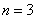 时,
时,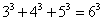 ,等式成立;
,等式成立;
当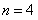 时,
时,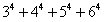 为偶数,而
为偶数,而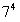 为奇数,
为奇数,
故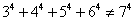 ,等式不成立;
,等式不成立;
当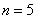 时,同
时,同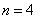 的情形可分析出,等式不成立
的情形可分析出,等式不成立
综上,所求的n只有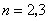 。
。

练习册系列答案
相关题目
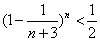 ,求证
,求证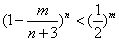 ,m=1,2,3,…,n;
,m=1,2,3,…,n;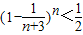 ,求证
,求证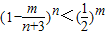 ,m=1,2…,n;
,m=1,2…,n;