题目内容
已知m,n为正整数,3m+n=20,则m>n的概率为
.
| 1 |
| 6 |
| 1 |
| 6 |
分析:用列举法求得所有的(m,n)共有6个,其中满足m>n的只有1个,由此求得m>n的概率.
解答:解:已知m,n为正整数,3m+n=20,则所有的(m,n)共有:(1,17)、(2,14)、(3,11)、(4,8)、(5,5)、(6,2),共计6个,
其中满足m>n的只有1个,故m>n的概率为
,
故答案为
.
其中满足m>n的只有1个,故m>n的概率为
| 1 |
| 6 |
故答案为
| 1 |
| 6 |
点评:本题考主要查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,列举法,是解决古典概型问题的一种重要的解题方法,属于基础题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
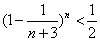 ,求证
,求证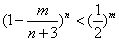 ,m=1,2,3,…,n;
,m=1,2,3,…,n;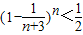 ,求证
,求证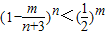 ,m=1,2…,n;
,m=1,2…,n;