题目内容
若不等式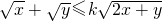 对于任意正实数x、y成立,则k的取值范围为 ________.
对于任意正实数x、y成立,则k的取值范围为 ________.

分析:将不等式
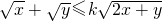 转化为k2≥
转化为k2≥ .只要求得
.只要求得 最大值即可.
最大值即可.解答:显然k>0,故k2≥
 .
.令t=
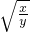 >0,则k2≥
>0,则k2≥
令u=4t+1>1,则t=
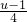 .
.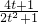 可转化为:s(u)=
可转化为:s(u)= ,
,于是,

 ≤
≤ (1+2)=
(1+2)= .
.∴k2≥
 ,即k≥
,即k≥ 时,不等式恒成立(当x=4y>0时等号成立).
时,不等式恒成立(当x=4y>0时等号成立).故答案为:

点评:本题考查将不等式的恒成立问题转化为求函数最值问题,求最值时一般是转化为基本函数解决,或用基本不等式,或用导数求解.

练习册系列答案
相关题目
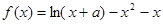 在点
在点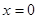 处取得极值。
处取得极值。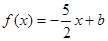 在区间[0,2]上有两个不等实根,求b的取值范围;
在区间[0,2]上有两个不等实根,求b的取值范围;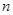 ,不等式
,不等式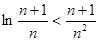 。
。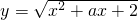 在区间(-∞,1]上是减函数,则实数a∈[-3,-2];
在区间(-∞,1]上是减函数,则实数a∈[-3,-2]; 对称.
对称.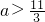 ;
;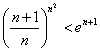 都成立.
都成立.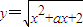 在区间(-∞,1]上是减函数,则实数a∈[-3,-2];
在区间(-∞,1]上是减函数,则实数a∈[-3,-2];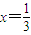 对称.
对称.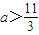 ;
;