题目内容
为研究重量x（单位：g）对弹簧长度y（单位：cm）的影响，对不同重量的6根弹簧进行测量，得如下数据：x | 5 | 10 | 15 | 20 | 25 | 30 |
y | 7.25 | 8.12 | 8.95 | 9.90 | 10.9 | 11.8 |
画出散点图，如果散点图中的各点大致分布在一条直线的附近，求y与x之间的回归直线方程.
解：散点图如下：
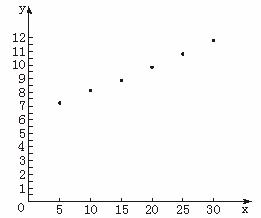
从散点图可看出，这是一个属于一元线性回归模型的问题.
此例中，n=6，计算可得
xi=105，
xi2=2275，
yi=59.92，
yi2=554.659，
xiyi=1076.2，
从而得
=17.5，
=9.487，
计算得b=0.183，a=6.284.
得到回归直线方程
=6.284+0.183x.
点评：两个变量是一对相关关系，但不一定就是线性相关关系，当散点图中的各点大致分布在一条直线附近时，求得的回归直线方程才是有意义的.
练习册系列答案
相关题目
为研究重量x(单位:g)对弹簧长度y(单位:cm)的影响,对承载不同重量的6根弹簧进行测量,数据如下表:
x | 5 | 10 | 15 | 20 | 25 | 30 |
y | 7.25 | 8.12 | 8.95 | 9.90 | 10.9 | 11.8 |
(1)画出散点图;
(2)如果散点图中的各点大致分布在一条直线的附近,求y与x之间的回归直线方程.
为研究重量x(单位：克)对弹簧长度y(单位：厘米)的影响,对不同重量的6根弹簧进行测量,得如下数据：
x | 5 | 10 | 15 | 20 | 25 | 30 |
y | 7.25 | 8.12 | 8.95 | 9.90 | 10.9 | 11.8 |
（1）画出散点图；
（2）如果散点图中的各点大致分布在一条直线的附过，求y与x之间的回归直线方程；
（3）对x、y两个变量进行相关性检验.