题目内容
已知向量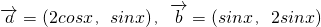 定义
定义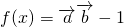 .
.
(1)求函数y=f(x),x∈R的单调递减区间;
(2)若函数 为偶函数,求θ的值.
为偶函数,求θ的值.
解:(1)函数y=f(x)= =2sinxcosx+2sin2x-1=sin2x-cos2x=
=2sinxcosx+2sin2x-1=sin2x-cos2x= sin(2x-
sin(2x- ).
).
令 2kπ+ ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,解得 kπ+
,k∈z,解得 kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈z.
,k∈z.
故函数的减区间为[kπ+ ,kπ+
,kπ+ ],k∈z.
],k∈z.
(2)若函数 为偶函数,则y=
为偶函数,则y= sin[2(x+θ)-
sin[2(x+θ)- ]=
]= sin(2x+2θ-
sin(2x+2θ- )为偶函数.
)为偶函数.
再由 可得 2θ-
可得 2θ- =
= ,
,
∴θ= .
.
分析:(1)利用两个向量的数量积公式,以及三角函数的恒等变换化简函数的解析式为 sin(2x-
sin(2x- ),根据 2kπ+
),根据 2kπ+ ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z求出函数的减区间.
,k∈z求出函数的减区间.
(2)由题意可得 y= sin[2(x+θ)-
sin[2(x+θ)- ]为偶函数,再由
]为偶函数,再由  可得 2θ-
可得 2θ- =
= ,由此求得 θ的值.
,由此求得 θ的值.
点评:本题主要考查两个向量的数量积公式,三角函数的恒等变换,正弦函数的单调性,属于中档题.
 =2sinxcosx+2sin2x-1=sin2x-cos2x=
=2sinxcosx+2sin2x-1=sin2x-cos2x= sin(2x-
sin(2x- ).
).令 2kπ+
 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,解得 kπ+
,k∈z,解得 kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈z.
,k∈z.故函数的减区间为[kπ+
 ,kπ+
,kπ+ ],k∈z.
],k∈z.(2)若函数
 为偶函数,则y=
为偶函数,则y= sin[2(x+θ)-
sin[2(x+θ)- ]=
]= sin(2x+2θ-
sin(2x+2θ- )为偶函数.
)为偶函数.再由
 可得 2θ-
可得 2θ- =
= ,
,∴θ=
 .
.分析:(1)利用两个向量的数量积公式,以及三角函数的恒等变换化简函数的解析式为
 sin(2x-
sin(2x- ),根据 2kπ+
),根据 2kπ+ ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z求出函数的减区间.
,k∈z求出函数的减区间.(2)由题意可得 y=
 sin[2(x+θ)-
sin[2(x+θ)- ]为偶函数,再由
]为偶函数,再由  可得 2θ-
可得 2θ- =
= ,由此求得 θ的值.
,由此求得 θ的值.点评:本题主要考查两个向量的数量积公式,三角函数的恒等变换,正弦函数的单调性,属于中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目