题目内容
(本小题满分12分)
已知等差数列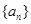 的公差为2,前
的公差为2,前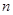 项和为
项和为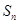 ,且
,且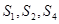 成等比数列.
成等比数列.
(Ⅰ)求数列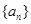 的通项公式;
的通项公式;
(Ⅱ)令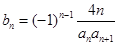 ,求数列
,求数列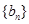 的前
的前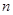 项和
项和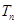 .
.
(I) .
.
(II) ,(或
,(或 )
)
解析试题分析:(I)因为 ,
, ,
,
由题意,得 ,
,
解得 ,
,
所以 .
.
(II)

当n为偶数时,


当n为奇数时,


所以 ,(或
,(或 )
)
试题解析:(I)因为 ,
, ,
,
由题意,得 ,
,
解得 ,
,
所以 .
.
(II)

当n为偶数时,


当n为奇数时,


所以 ,(或
,(或 )
)
考点:等差数列的前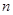 项和,等比数列及其性质,“裂项相消法”,分类讨论思想.
项和,等比数列及其性质,“裂项相消法”,分类讨论思想.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
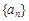 的前n项和为
的前n项和为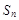 ,且
,且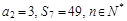
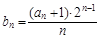 ,求数列
,求数列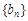 的前n项和Tn.
的前n项和Tn.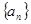 中,
中,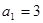 ,其前
,其前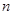 项和为
项和为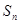 ,等比数列
,等比数列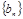 的各项均为正数,
的各项均为正数,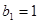 ,公比为
,公比为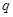 ,且
,且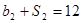 ,
,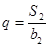 .
.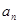 与
与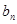 ; (2)设数列
; (2)设数列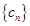 满足
满足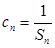 ,求
,求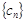 的前
的前 .
.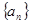 满足:
满足: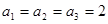 ,
,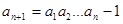 (
(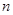 ≥3),记
≥3),记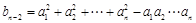
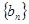 为等差数列,并求通项公式;
为等差数列,并求通项公式;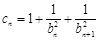 ,数列{
,数列{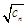 }的前n项和为
}的前n项和为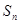 ,求证:
,求证: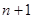 .
. +n-4.
+n-4. 的前
的前 项和为
项和为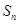 ,已知
,已知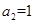 ,
,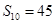 .
. 满足
满足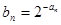 ,求数列
,求数列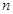 项和
项和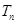 .
.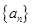 的前
的前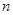 项和为
项和为 ,且对任意的
,且对任意的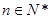 ,都有
,都有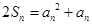 。
。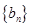 满足
满足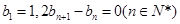 ,且cn=anbn,求数列
,且cn=anbn,求数列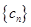 的前
的前 ;
;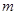 ,使得对任意的正整数
,使得对任意的正整数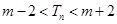 ,若存在,求出
,若存在,求出 的取值范围;
的取值范围;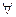 n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列.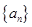 是等差数列,满足
是等差数列,满足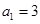 ,
, ,数列
,数列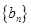 满足
满足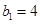 ,
,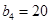 ,且
,且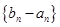 是等比数列.
是等比数列.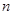 项和.
项和.