Question

设cosα=,tanβ=,π＜α＜,0＜β＜,求α-β的值.

Answer 1

解法一:由cosα=,π＜α＜,得sinα=-,tanα=2.又tanβ=,

于是tan(α-β)=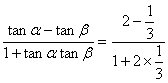=1.

又由π＜α＜,0＜β＜,可得-＜-β＜0, ＜α-β＜,

因此,α-β=.

解法二:由cosα=,π＜α＜,得sinα=-.

由tanβ=,0＜β＜,得sinβ=,cosβ=.

所以sin(α-β)=sinαcosβ-cosαsinβ=(-)()-()()=-.

又由π＜α＜,0＜β＜,可得-＜-β＜0, ＜α-β＜,因此,α-β=.