Question

设cosα=-,tanβ=,π＜α＜,0＜β＜.求α-β的值.

Answer 1

解法1：∵π＜α＜,0＜β＜,

∴＜α-β＜,于是选择α-β的正弦函数值.

∵cosα=-,π＜α＜，

∴sinα=-.

∵tanβ＝,0＜β＜,

∴cos²β=，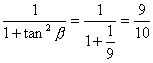

即cosβ=,sinβ=.

∴sin(α-β)=sinαcosβ-cosαsinβ

=-×-(-)×=-.

∵＜α-β＜,

∴α-β=.

解法2：以上同解法1.

∵cos(α-β)=cosαcosβ+sinαsinβ

=-×+(-)×=-.

∵tanβ=＜1,

∴0＜β＜.

∴＜α-β＜.

∴α-β=.

解法3：∵cosα=-,π＜α＜,

∴sinα=-.

∴tanα=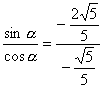=2.

则tan(α-β)=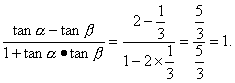

∵π＜α＜,0＜β＜,

∴＜α-β＜.

∴α-β=.

说明：本题选择正弦函数、正切函数都比较简单，因为这两个函数在α-β∈(,)上是单调的，即求得的角只有一个解，省去缩小角的范围的麻烦，而选择余弦函数，由于它在（,）上不单调，若不进一步缩小角的范围，就会产生增根.