题目内容
11.已知等比数列{an}中,a1=$\frac{1}{2}$,公比q=$\frac{1}{2}$.(1)Sn为{an}的前n项和;证明:Sn=1-an;
(2)设bn=log2a1+log2a2+…+log2an,求数列{bn}的通项公式.
分析 (1)分别由等比数列的通项公式和求和公式计算两边的式子,验证可得;
(2)由(1)和对数的运算可得log2an=-n,可得bn=-(1+2+3+…+n),由等差数列的求和公式可得.
解答 (1)证明:∵等比数列{an}中,a1=$\frac{1}{2}$,公比q=$\frac{1}{2}$,
∴Sn=$\frac{\frac{1}{2}[1-(\frac{1}{2})^{n}]}{1-\frac{1}{2}}$=1-($\frac{1}{2}$)n,1-an=1-$\frac{1}{2}$($\frac{1}{2}$)n-1=1-($\frac{1}{2}$)n,
∴Sn=1-an;
(2)解:由(1)可知an=($\frac{1}{2}$)n,故log2an=-n,
∴bn=log2a1+log2a2+…+log2an=-1+(-2)+(-3)+…+(-n)
=-(1+2+3+…+n)=-$\frac{n(1+n)}{2}$.
点评 本题考查等比数列的通项公式和求和公式,涉及等差数列的求和公式,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.不等式x2+x<$\frac{a}{b}$+$\frac{b}{a}$ 对任意a,b∈(0,+∞)恒成立,则实数x的取值范围是( )
| A. | (-2,0) | B. | (-∞,-2)∪(1,+∞) | C. | (-2,1) | D. | (-∞,-4)∪(2,+∞) |
16.如果x,y为实数,且x2-x+(y-1)2=0,则x的取值范围为( )
| A. | 任意实数 | B. | 负实数 | C. | 0<x≤$\frac{1}{2}$ | D. | 0≤x≤1 |
16.命题“?x∈R,f(x)g(x)≠0”的否定是( )
| A. | ?x∈R,f(x)=0且g(x)=0 | B. | ?x∈R,f(x)=0或g(x)=0 | ||
| C. | ?x0∈R,f(x0)=0且g(x0)=0 | D. | ?x0∈R,f(x0)=0或g(x0)=0 |
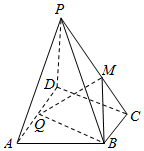 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点.