题目内容
已知向量
、
的夹角为60°，且||=2，||=1，若
，则m的值为
- A.3
- B.
- C.
- D.
B
分析：利用向量垂直的充要条件列出方程，利用多项式乘法展开，利用向量的数量积公式将方程表示成关于m的方程，求出m的值．
解答：∵
∴
即
即8m+m-2-1=0
解得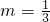
故选B
点评：解决向量垂直的问题一般利用向量垂直的充要条件：数量积为0；解决有关向量的模的问题常利用向量模的平方等于向量的平方．
分析：利用向量垂直的充要条件列出方程，利用多项式乘法展开，利用向量的数量积公式将方程表示成关于m的方程，求出m的值．
解答：∵
∴
即
即8m+m-2-1=0
解得
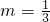
故选B
点评：解决向量垂直的问题一般利用向量垂直的充要条件：数量积为0；解决有关向量的模的问题常利用向量模的平方等于向量的平方．
练习册系列答案
相关题目
，
的夹角为
，且|
|=
，|
|=2．在△ABC中，
=2
+2
，
=2
-6
，D为BC边的中点，则|
|= ．